Journalisten und Statistik
In einem Presseartikel zum Thema Ungleichheit der Einkommensverteilung liest man folgendes
Blickt man auf bekannte Gleichheitsstudien, könnte man erwarten, dass die Ungleichheit in den Orten am höchsten ist, in denen die Menschen am wenigsten verdienen.
Ein Statistik-Student hätte bei so einer Formulierung schon ein Problem, die Prüfung über Statistik 1 noch positiv abzuschließen.
Es geht in dem Artikel um den Gini-Koeffizienten (in der deutschsprachigen Literatur heißt er auch Lorenz-Münzner-Koeffizient). Der misst die relative Ungleichheit.
Das Ergebnis der dort zitierten Studie der Wirtschaftsuniversität Wien ist, dass die Ungleichheit in reicheren Gemeinden eine höhere ist als in armen Gemeinden. Der Journalist schließt daraus, dass es auch in reicheren Gemeinden Arme geben muss.
Das ist aber nicht richtig.
Stellen wir uns eine Gemeinde A vor, in der es nur zwei Einkommensklassen gibt, und in der die Besserverdiener das
Doppelte der Schlechterverdiener verdienen. Zwei Drittel der Einkommensbezieher sind Schlechterverdierer.
In dieser Gemeinde beträgt der Gini-Koeffizient 0,33.
In einer anderen Gemeinde B verdienen die Besserverdiener das Fünffache der Schlechterverdiener, und auch dort sind die Schlechterverdiener zwei Drittel aller Einkommensbezieher. In dieser Gemeinde beträgt der Gini-Koeffizient 0,5.
Der Gini-Koeffizient ist unabhängig von der Höhe der Durchschnittseinkommen in den beiden Gemeinden. Auch wenn die Schlechterverdiener in Gemeinde B deutlich besser verdienen als die Besserverdiener in Gemeinde A, ist der der Gini-Koeffizient in Gemeinde B höher als in Gemeinde A. Dabei verdient trotz der höheren Ungleichheit jeder Einkommensbezieher in Gemeinde B mehr als jeder Einkommensbezieher in Gemeinde A!
Um in der Analogie des Journalisten zu bleiben:
In diesem Szenario gehen also in der Gemeinde B nicht Kinder von ärmeren und reicheren Österreichern in dieselbe Schule. Man könnte vereinfachend sagen, dass da Kinder von Reichen mit Kindern von extrem Reichen in die Schule gehen, während in Gemeinde A Kinder von armen mit Kindern von halbwegs Wohlhabenden in die Schule gehen.
Bei dem zitierten Artikel ist die Versuchung, ein bekanntes Kreisky-Zitat zu variieren, sehr groß:
Lernen sie Statistik, Herr Redakteur!
PISA-Scores aller teilnehmende Länder
In vielen Diskussionen wird mit Verbesserungen und Verschlechterungen der PISA-Werte verschiedender Länder argumentiert. Eine vollständige Übersicht über alle PISA-Werte ist aber schwer zu finden (auch auf den PISA-OECD-Websites findet man keine umfassende Darstellung).
Die folgenden Tabellen enthalten die PISA-Länderscores für alle Länder, die irgendwann an einem PISA-Test teilgenommen haben.
Die Tabellen weisen für Länder, die mehrfach teilgenommen haben, auch den Unterschied für den größten und den kleinsten PISA-Score aus.
Die OECD sagt, dass Längsschnittvergleiche immer erst ab jenem Zeitpunkt durchgeführt werden sollen, wo eine Domäne Hauptdomäne war. Da das bei Lesen 2000, bei Mathematik 2003 und bei den Naturwissenschaften 2006 der Fall war, weist die letzte Spalte in jeder Tabelle die Veränderung zwischen diesem Zeitpunkt und 2012 aus. So können wir längerfristige Veränderungen für die einzelnen Länder untersuchen. Als Hinweis darauf, dass manche Ergebnisse nicht zuverlässig genug für Langfristvergleiche sind, sind die entsprechenden Spalten der Tabellen kursiv gesetzt.
Durch Klicken auf den Tabellenkopf kann man die Tabellen nach den einzelnen Spalten sortieren und so zum Beispiel einfach herausfinden, welches Land von 2000 auf 2012 den stärksten Leistungsabfall im Lesen hatte (Schweden).
Auch in Mathematik und den Naturwissenschaften hatte Schweden den stärksten Leistungsabfall vom Verankerungszeitpunkt (2003 bzw. 2006) zum letzten Test 2012.
Ländermittelwerte Lesen
| country | read 2000 | read 2003 | read 2006 | read 2009 | read 2012 | max-min | 2000 -> 2012 |
|---|---|---|---|---|---|---|---|
| Albania | 348.8 | 384.8 | 394.0 | 45.1 | 45.1 | ||
| Argentina | 418.3 | 373.7 | 398.3 | 396.0 | 44.5 | -22.3 | |
| Australia | 528.3 | 525.4 | 512.9 | 514.9 | 511.8 | 16.5 | -16.5 |
| Austria | 492.1 | 490.7 | 490.2 | 470.3 | 489.6 | 21.8 | -2.4 |
| Azerbaijan | 352.9 | 361.5 | 8.6 | ||||
| Belgium | 507.1 | 507.0 | 500.9 | 505.9 | 508.6 | 7.7 | 1.5 |
| Brazil | 396.0 | 402.8 | 392.9 | 411.8 | 406.5 | 18.9 | 10.5 |
| Bulgaria | 430.4 | 401.9 | 429.1 | 436.1 | 34.2 | 5.7 | |
| Canada | 534.3 | 527.9 | 527.0 | 524.2 | 523.1 | 11.2 | -11.2 |
| Chile | 409.6 | 442.1 | 449.4 | 441.4 | 39.8 | 31.8 | |
| Chinese Taipei | 496.2 | 495.2 | 523.1 | 27.9 | |||
| Colombia | 385.3 | 413.2 | 403.4 | 27.9 | |||
| Connecticut (USA) | 521.2 | ||||||
| Costa Rica | 442.6 | 440.5 | 2.0 | ||||
| Croatia | 477.4 | 475.7 | 484.6 | 8.8 | |||
| Czech Rep. | 491.6 | 488.5 | 482.7 | 478.2 | 492.9 | 14.7 | 1.3 |
| Denmark | 496.9 | 492.3 | 494.5 | 494.9 | 496.1 | 4.5 | -0.7 |
| Estonia | 500.7 | 501.0 | 516.3 | 15.5 | |||
| Finland | 546.5 | 543.5 | 546.9 | 535.9 | 524.0 | 22.8 | -22.4 |
| Florida (USA) | 492.1 | ||||||
| France | 504.7 | 496.2 | 487.7 | 495.6 | 505.5 | 17.8 | 0.7 |
| Georgia | 374.3 | ||||||
| Germany | 484.0 | 491.4 | 494.9 | 497.3 | 507.7 | 23.7 | 23.7 |
| Greece | 473.8 | 472.3 | 459.7 | 482.8 | 477.2 | 23.1 | 3.4 |
| Hong Kong-China | 525.5 | 509.5 | 536.1 | 533.2 | 544.6 | 35.1 | 19.1 |
| Hungary | 480.0 | 481.9 | 482.4 | 494.2 | 488.5 | 14.2 | 8.5 |
| Iceland | 506.9 | 491.7 | 484.4 | 500.3 | 482.5 | 24.4 | -24.4 |
| India | 334.6 | ||||||
| Indonesia | 370.6 | 381.6 | 392.9 | 401.7 | 396.1 | 31.1 | 25.5 |
| Ireland | 526.7 | 515.5 | 517.3 | 495.6 | 523.2 | 31.0 | -3.5 |
| Israel | 452.2 | 438.7 | 474.0 | 485.8 | 47.1 | 33.6 | |
| Italy | 487.5 | 475.7 | 468.5 | 486.1 | 489.8 | 21.2 | 2.3 |
| Japan | 522.2 | 498.1 | 498.0 | 519.9 | 538.1 | 40.1 | 15.8 |
| Jordan | 400.6 | 405.0 | 399.0 | 6.0 | |||
| Kazakhstan | 390.4 | 392.7 | 2.3 | ||||
| Korea | 524.8 | 534.1 | 556.0 | 539.3 | 535.8 | 31.3 | 11.0 |
| Kyrgyzstan | 284.7 | 314.0 | 29.3 | ||||
| Latvia | 458.1 | 490.6 | 479.5 | 484.0 | 488.7 | 32.5 | 30.6 |
| Liechtenstein | 482.6 | 525.1 | 510.4 | 499.3 | 515.5 | 42.5 | 32.9 |
| Lithuania | 470.1 | 468.4 | 477.3 | 8.9 | |||
| Luxembourg | 441.2 | 479.4 | 479.4 | 472.2 | 487.8 | 46.6 | 46.6 |
| Macao-China | 497.6 | 492.3 | 486.6 | 508.9 | 22.3 | ||
| Macedonia | 372.5 | ||||||
| Malaysia | 413.8 | 398.2 | 15.6 | ||||
| Malta | 442.1 | ||||||
| Massachusetts (USA) | 527.1 | ||||||
| Mauritius | 406.6 | ||||||
| Mexico | 422.0 | 399.7 | 410.5 | 425.3 | 423.6 | 25.5 | 1.6 |
| Miranda-Venezuela | 421.8 | ||||||
| Montenegro | 392.0 | 407.5 | 422.1 | 30.1 | |||
| Netherlands | 531.9 | 513.1 | 506.7 | 508.4 | 511.2 | 25.2 | -20.7 |
| New Zealand | 528.8 | 521.6 | 521.0 | 520.9 | 512.2 | 16.6 | -16.6 |
| Norway | 505.3 | 499.7 | 484.3 | 503.2 | 503.9 | 21.0 | -1.3 |
| Panama | 370.7 | ||||||
| Peru | 327.1 | 369.7 | 384.2 | 57.1 | 57.1 | ||
| Poland | 479.1 | 496.6 | 507.6 | 500.5 | 518.2 | 39.1 | 39.1 |
| Portugal | 470.2 | 477.6 | 472.3 | 489.3 | 487.8 | 19.2 | 17.6 |
| Qatar | 312.2 | 371.7 | 387.5 | 75.3 | |||
| Rep. of Moldova | 388.1 | ||||||
| Romania | 427.9 | 395.9 | 424.5 | 437.6 | 41.7 | 9.7 | |
| Russian Federation | 461.8 | 442.2 | 439.9 | 459.4 | 475.1 | 35.3 | 13.4 |
| Serbia | 401.0 | 442.0 | 446.1 | 45.1 | |||
| Shanghai-China | 555.8 | 569.6 | 13.8 | ||||
| Singapore | 525.9 | 542.2 | 16.3 | ||||
| Slovak Rep. | 469.2 | 466.3 | 477.4 | 462.8 | 14.7 | ||
| Slovenia | 494.4 | 483.1 | 481.3 | 13.1 | |||
| Spain | 492.6 | 480.5 | 460.8 | 481.0 | 487.9 | 31.7 | -4.6 |
| Sweden | 516.3 | 514.3 | 507.3 | 497.4 | 483.3 | 33.0 | -33.0 |
| Switzerland | 494.4 | 499.1 | 499.3 | 500.5 | 509.0 | 14.7 | 14.7 |
| Thailand | 430.7 | 419.9 | 416.8 | 421.4 | 441.2 | 24.5 | 10.5 |
| Trinidad and Tobago | 416.5 | ||||||
| Tunisia | 374.6 | 380.3 | 403.6 | 404.1 | 29.5 | ||
| Turkey | 441.0 | 447.1 | 464.2 | 475.5 | 34.5 | ||
| United Arab Em. | 431.4 | 441.7 | 10.3 | ||||
| United Kingdom | 523.4 | 507.0 | 495.1 | 494.2 | 499.3 | 29.3 | -24.1 |
| United States | 504.4 | 495.2 | 499.8 | 497.6 | 9.2 | -6.8 | |
| Uruguay | 434.1 | 412.5 | 425.8 | 411.3 | 22.8 | ||
| Yugoslavia | 411.7 |
Ländermittelwerte Mathematik
| country | math 2000 | math03 | math 2006 | math 2009 | math 2012 | max- min | 2003 -> 2012 |
|---|---|---|---|---|---|---|---|
| Albania | 381.2 | 377.5 | 394.3 | 16.9 | |||
| Argentina | 387.6 | 381.3 | 388.1 | 388.4 | 7.2 | ||
| Australia | 533.3 | 524.3 | 519.9 | 514.3 | 504.2 | 29.2 | -20.1 |
| Austria | 502.5 | 505.6 | 505.5 | 495.9 | 505.5 | 9.7 | -0.1 |
| Azerbaijan | 476.0 | 431.0 | 45.0 | ||||
| Belgium | 519.6 | 529.3 | 520.3 | 515.3 | 514.5 | 14.8 | -14.8 |
| Brazil | 333.9 | 356.0 | 369.5 | 385.8 | 388.5 | 54.6 | 32.5 |
| Bulgaria | 429.6 | 413.4 | 428.1 | 438.7 | 25.3 | ||
| Canada | 533.0 | 532.5 | 527.0 | 526.8 | 518.1 | 14.9 | -14.4 |
| Chile | 383.5 | 411.4 | 421.1 | 422.6 | 39.1 | ||
| Chinese Taipei | 549.4 | 543.2 | 559.8 | 16.6 | |||
| Colombia | 370.0 | 380.8 | 376.5 | 10.9 | |||
| Connecticut (USA) | 505.8 | ||||||
| Costa Rica | 409.4 | 407.0 | 2.4 | ||||
| Croatia | 467.2 | 459.9 | 471.1 | 11.2 | |||
| Czech Republic | 497.6 | 516.5 | 509.9 | 492.8 | 499.0 | 23.6 | -17.5 |
| Denmark | 514.5 | 514.3 | 513.0 | 503.3 | 500.0 | 14.5 | -14.3 |
| Estonia | 514.6 | 512.1 | 520.5 | 8.4 | |||
| Finland | 536.2 | 544.3 | 548.4 | 540.5 | 518.8 | 29.6 | -25.5 |
| Florida (USA) | 466.8 | ||||||
| France | 517.2 | 510.8 | 495.5 | 496.8 | 495.0 | 22.2 | -15.8 |
| Georgia | 379.5 | ||||||
| Germany | 489.8 | 503.0 | 503.8 | 512.8 | 513.5 | 23.7 | 10.5 |
| Greece | 446.9 | 444.9 | 459.2 | 466.1 | 453.0 | 21.2 | 8.1 |
| Hong Kong-China | 560.5 | 550.4 | 547.5 | 554.5 | 561.2 | 13.8 | 10.8 |
| Hungary | 488.0 | 490.0 | 490.9 | 490.2 | 477.0 | 13.9 | -13.0 |
| Iceland | 514.4 | 515.1 | 505.5 | 506.7 | 492.8 | 22.3 | -22.3 |
| India | 349.4 | ||||||
| Indonesia | 366.7 | 360.2 | 391.0 | 371.3 | 375.1 | 30.8 | 14.9 |
| Ireland | 502.9 | 502.8 | 501.5 | 487.1 | 501.5 | 15.8 | -1.3 |
| Israel | 433.0 | 441.9 | 446.9 | 466.5 | 33.5 | ||
| Italy | 457.3 | 465.7 | 461.7 | 482.9 | 485.3 | 28.0 | 19.6 |
| Japan | 556.6 | 534.1 | 523.1 | 529.0 | 536.4 | 33.5 | 2.3 |
| Jordan | 384.0 | 386.7 | 385.6 | 2.6 | |||
| Kazakhstan | 404.9 | 431.8 | 26.9 | ||||
| Korea | 546.8 | 542.2 | 547.5 | 546.2 | 553.8 | 11.5 | 11.6 |
| Kyrgyzstan | 310.6 | 331.2 | 20.6 | ||||
| Latvia | 462.8 | 483.4 | 486.2 | 482.0 | 490.6 | 27.8 | 7.2 |
| Liechtenstein | 514.1 | 535.8 | 525.0 | 536.0 | 535.0 | 22.0 | -0.8 |
| Lithuania | 486.4 | 476.6 | 478.8 | 9.8 | |||
| Luxembourg | 445.7 | 493.2 | 490.0 | 489.1 | 489.8 | 47.6 | -3.4 |
| Macao-China | 527.3 | 525.0 | 525.3 | 538.1 | 13.1 | 10.8 | |
| Macedonia | 381.3 | ||||||
| Malaysia | 404.3 | 420.5 | 16.3 | ||||
| Malta | 462.9 | ||||||
| Massachusetts (USA) | 513.5 | ||||||
| Mauritius | 420.0 | ||||||
| Mexico | 387.3 | 385.2 | 405.7 | 418.5 | 413.3 | 33.3 | 28.1 |
| Miranda-Venezuela | 396.9 | ||||||
| Montenegro | 399.3 | 402.5 | 409.6 | 10.3 | |||
| Netherlands | 563.8 | 537.8 | 530.7 | 525.8 | 523.0 | 40.8 | -14.8 |
| New Zealand | 536.9 | 523.5 | 522.0 | 519.3 | 499.7 | 37.1 | -23.8 |
| Norway | 499.4 | 495.2 | 489.8 | 498.0 | 489.4 | 10.0 | -5.8 |
| Panama | 359.7 | ||||||
| Peru | 292.1 | 365.1 | 368.1 | 76.0 | |||
| Poland | 470.1 | 490.2 | 495.4 | 494.8 | 517.5 | 47.4 | 27.3 |
| Portugal | 453.7 | 466.0 | 466.2 | 486.9 | 487.1 | 33.3 | 21.1 |
| Qatar | 318.0 | 368.1 | 376.4 | 58.5 | |||
| Republic of Moldova | 397.5 | ||||||
| Romania | 425.5 | 414.8 | 427.1 | 444.6 | 29.8 | ||
| Russian Federation | 478.3 | 468.4 | 475.7 | 467.8 | 482.2 | 14.4 | 13.8 |
| Serbia | 435.4 | 442.4 | 448.9 | 13.5 | |||
| Shanghai-China | 600.1 | 612.7 | 12.6 | ||||
| Singapore | 562.0 | 573.5 | 11.4 | ||||
| Slovak Republic | 498.2 | 492.1 | 496.7 | 481.6 | 16.5 | -16.6 | |
| Slovenia | 504.5 | 501.5 | 501.1 | 3.3 | |||
| Spain | 476.3 | 485.1 | 480.0 | 483.5 | 484.3 | 8.8 | -0.8 |
| Sweden | 509.8 | 509.0 | 502.4 | 494.2 | 478.3 | 31.5 | -30.7 |
| Switzerland | 529.3 | 526.6 | 529.7 | 534.0 | 530.9 | 7.4 | 4.3 |
| Thailand | 432.3 | 417.0 | 417.1 | 418.6 | 426.7 | 15.3 | 9.7 |
| Trinidad and Tobago | 414.0 | 0.0 | |||||
| Tunisia | 358.7 | 365.5 | 371.5 | 387.8 | 29.1 | 29.1 | |
| Turkey | 423.4 | 423.9 | 445.5 | 448.0 | 24.6 | 24.6 | |
| United Arab Emirates | 421.1 | 434.0 | 12.9 | ||||
| United Kingdom | 529.2 | 508.3 | 495.4 | 492.4 | 493.9 | 36.8 | -14.4 |
| United States | 493.2 | 482.9 | 474.4 | 487.4 | 481.4 | 18.8 | -1.5 |
| Uruguay | 422.2 | 426.8 | 426.7 | 409.3 | 17.5 | -12.9 | |
| Yugoslavia | 436.9 |
Ländermittelwerte Naturwissenschaften
| country | scie 2000 | scie 2003 | scie 2006 | scie 2009 | scie 2012 | max- min | 2006 -> 2012 |
|---|---|---|---|---|---|---|---|
| Albania | 383.3 | 390.7 | 397.4 | 14.1 | |||
| Argentina | 396.8 | 391.2 | 400.8 | 405.6 | 14.4 | 14.4 | |
| Australia | 528.1 | 525.1 | 526.9 | 527.3 | 521.5 | 6.6 | -5.4 |
| Austria | 496.4 | 491.0 | 510.8 | 494.3 | 505.8 | 19.9 | -5.0 |
| Azerbaijan | 382.3 | 373.2 | 9.2 | ||||
| Belgium | 488.0 | 508.8 | 510.4 | 506.6 | 504.9 | 22.4 | -5.5 |
| Brazil | 377.7 | 389.6 | 390.3 | 405.4 | 401.6 | 27.7 | 11.3 |
| Bulgaria | 458.1 | 434.1 | 439.3 | 446.5 | 24.0 | 12.4 | |
| Canada | 533.4 | 518.7 | 534.5 | 528.7 | 525.4 | 15.7 | -9.1 |
| Chile | 412.9 | 438.2 | 447.5 | 444.9 | 34.6 | 6.7 | |
| Chinese Taipei | 532.5 | 520.4 | 523.3 | 12.1 | -9.2 | ||
| Colombia | 388.0 | 401.8 | 398.7 | 13.7 | 10.7 | ||
| Connecticut (USA) | 520.8 | ||||||
| Costa Rica | 430.5 | 429.4 | 1.1 | ||||
| Croatia | 493.2 | 486.4 | 491.4 | 6.8 | -1.8 | ||
| Czech Republic | 502.9 | 523.3 | 512.9 | 500.5 | 508.3 | 22.8 | -4.6 |
| Denmark | 479.6 | 475.2 | 495.9 | 499.3 | 498.5 | 24.1 | 2.6 |
| Estonia | 531.4 | 527.8 | 541.4 | 13.6 | 10.0 | ||
| Finland | 530.0 | 548.2 | 563.3 | 554.1 | 545.4 | 33.3 | -17.9 |
| Florida (USA) | 485.0 | ||||||
| France | 497.5 | 511.2 | 495.2 | 498.2 | 499.0 | 16.0 | 3.8 |
| Georgia | 372.7 | ||||||
| Germany | 476.5 | 502.3 | 515.6 | 520.4 | 524.1 | 47.7 | 8.5 |
| Greece | 479.5 | 481.0 | 473.4 | 470.1 | 466.7 | 14.3 | -6.7 |
| Hong Kong-China | 541.4 | 539.5 | 542.2 | 549.0 | 554.9 | 15.4 | 12.7 |
| Hungary | 489.8 | 503.3 | 503.9 | 502.6 | 494.3 | 14.1 | -9.6 |
| Iceland | 493.7 | 494.7 | 490.8 | 495.6 | 478.2 | 17.4 | -12.6 |
| India | 346.0 | ||||||
| Indonesia | 401.4 | 395.0 | 393.5 | 382.6 | 381.9 | 19.5 | -11.6 |
| Ireland | 508.1 | 505.4 | 508.3 | 508.0 | 522.0 | 16.6 | 13.7 |
| Israel | 453.0 | 453.9 | 454.9 | 470.1 | 17.1 | 16.2 | |
| Italy | 478.5 | 486.5 | 475.4 | 488.8 | 493.5 | 18.1 | 18.1 |
| Japan | 554.5 | 547.6 | 531.4 | 539.4 | 546.7 | 23.1 | 15.3 |
| Jordan | 422.0 | 415.4 | 409.4 | 12.6 | -12.6 | ||
| Kazakhstan | 400.4 | 424.7 | 24.3 | ||||
| Korea | 556.4 | 538.4 | 522.1 | 538.0 | 537.8 | 34.2 | 15.7 |
| Kyrgyzstan | 322.0 | 329.5 | 7.5 | ||||
| Latvia | 465.0 | 489.1 | 489.5 | 493.9 | 502.2 | 37.2 | 12.7 |
| Liechtenstein | 473.3 | 525.2 | 522.2 | 519.9 | 524.7 | 51.9 | 2.5 |
| Lithuania | 488.0 | 491.4 | 495.7 | 7.7 | 7.7 | ||
| Luxembourg | 447.1 | 482.8 | 486.3 | 483.9 | 491.2 | 44.1 | 4.9 |
| Macao-China | 524.7 | 510.8 | 511.1 | 520.6 | 13.8 | 9.8 | |
| Macedonia | 406.5 | 0.0 | |||||
| Malaysia | 422.2 | 419.5 | 2.7 | ||||
| Malta | 461.3 | ||||||
| Massachusetts (USA) | 527.4 | ||||||
| Mauritius | 417.2 | ||||||
| Mexico | 420.6 | 404.9 | 409.7 | 415.9 | 414.9 | 15.7 | 5.2 |
| Miranda-Venezuela | 421.6 | ||||||
| Montenegro | 411.8 | 401.3 | 410.1 | 10.5 | -1.7 | ||
| Netherlands | 528.5 | 524.4 | 524.9 | 522.2 | 522.1 | 6.4 | -2.8 |
| New Zealand | 526.9 | 520.9 | 530.4 | 532.0 | 515.6 | 16.4 | -14.8 |
| Norway | 496.4 | 484.2 | 486.5 | 499.9 | 494.5 | 15.7 | 8.0 |
| Panama | 375.9 | ||||||
| Peru | 335.4 | 369.4 | 373.1 | 37.8 | |||
| Poland | 489.9 | 497.8 | 497.8 | 508.1 | 525.8 | 36.0 | 28.0 |
| Portugal | 451.4 | 467.7 | 474.3 | 492.9 | 489.3 | 41.6 | 15.0 |
| Qatar | 349.3 | 379.4 | 383.6 | 34.3 | 34.3 | ||
| Republic of Moldova | 412.8 | ||||||
| Romania | 448.1 | 418.4 | 428.2 | 438.8 | 29.7 | 20.4 | |
| Russian Federation | 463.1 | 489.3 | 479.5 | 478.3 | 486.3 | 26.2 | 6.8 |
| Serbia | 435.6 | 442.8 | 444.8 | 9.2 | 9.2 | ||
| Shanghai-China | 574.6 | 580.1 | 5.5 | ||||
| Singapore | 541.7 | 551.5 | 9.8 | ||||
| Slovak Republic | 494.9 | 488.4 | 490.3 | 471.2 | 23.7 | -17.2 | |
| Slovenia | 518.8 | 511.8 | 514.1 | 7.1 | -4.7 | ||
| Spain | 492.2 | 487.1 | 488.4 | 488.3 | 496.4 | 9.4 | 8.0 |
| Sweden | 510.0 | 506.1 | 503.3 | 495.1 | 484.8 | 25.2 | -18.5 |
| Switzerland | 498.5 | 513.0 | 511.5 | 516.6 | 515.3 | 18.1 | 3.8 |
| Thailand | 437.5 | 429.1 | 421.0 | 425.3 | 444.0 | 23.0 | 23.0 |
| Trinidad and Tobago | 410.2 | ||||||
| Tunisia | 384.7 | 385.5 | 400.7 | 398.0 | 16.0 | 12.5 | |
| Turkey | 434.2 | 423.8 | 453.9 | 463.4 | 39.6 | 39.6 | |
| United Arab Emirates | 437.8 | 448.4 | 10.6 | ||||
| United Kingdom | 533.4 | 518.4 | 514.8 | 513.7 | 514.1 | 19.7 | -0.7 |
| United States | 504.7 | 491.3 | 488.9 | 502.0 | 497.4 | 15.8 | 8.5 |
| Uruguay | 438.4 | 428.1 | 427.2 | 415.8 | 22.5 | -12.3 | |
| Yugoslavia | 436.4 |
Zur statistischen Beurteilung und Berechnung von Tests braucht man auch die Standardfehler (se = standard error) der einzelnen Länder. In den folgenden drei Tabellen findet man diese Werte.
Standardfehler Ländermittelwerte Lesen
| country | se read 2000 | se read 2003 | se read 2006 | se read 2009 | se read 2012 |
|---|---|---|---|---|---|
| Albania | 3.3 | 4.0 | 3.2 | ||
| Argentina | 9.9 | 7.2 | 4.6 | 3.7 | |
| Australia | 3.5 | 2.1 | 2.1 | 2.3 | 1.6 |
| Austria | 2.7 | 3.8 | 4.1 | 2.9 | 2.8 |
| Azerbaijan | 3.1 | 3.3 | |||
| Belgium | 3.6 | 2.6 | 3.0 | 2.3 | 2.3 |
| Brazil | 3.1 | 4.6 | 3.7 | 2.7 | 2.0 |
| Bulgaria | 4.9 | 6.9 | 6.7 | 6.0 | |
| Canada | 1.6 | 1.7 | 2.4 | 1.5 | 1.9 |
| Chile | 3.6 | 5.0 | 3.1 | 2.9 | |
| Chinese Taipei | 3.4 | 2.6 | 3.0 | ||
| Colombia | 5.1 | 3.7 | 3.4 | ||
| Connecticut (USA) | 6.5 | ||||
| Costa Rica | 3.2 | 3.5 | |||
| Croatia | 2.8 | 2.9 | 3.3 | ||
| Czech Republic | 2.4 | 3.5 | 4.2 | 2.9 | 2.9 |
| Denmark | 2.4 | 2.8 | 3.2 | 2.1 | 2.6 |
| Estonia | 2.9 | 2.6 | 2.0 | ||
| Finland | 2.6 | 1.6 | 2.1 | 2.3 | 2.4 |
| Florida (USA) | 6.1 | ||||
| France | 2.7 | 2.7 | 4.1 | 3.4 | 2.8 |
| Georgia | 2.9 | ||||
| Germany | 2.5 | 3.4 | 4.4 | 2.7 | 2.8 |
| Greece | 5.0 | 4.1 | 4.0 | 4.3 | 3.3 |
| Hong Kong-China | 2.9 | 3.7 | 2.4 | 2.1 | 2.8 |
| Hungary | 4.0 | 2.5 | 3.3 | 3.2 | 3.2 |
| Iceland | 1.5 | 1.6 | 1.9 | 1.4 | 1.8 |
| India | 4.9 | ||||
| Indonesia | 4.0 | 3.4 | 5.9 | 3.7 | 4.2 |
| Ireland | 3.2 | 2.6 | 3.5 | 3.0 | 2.6 |
| Israel | 8.5 | 4.6 | 3.6 | 5.0 | |
| Italy | 2.9 | 3.0 | 2.4 | 1.6 | 2.0 |
| Japan | 5.2 | 3.9 | 3.6 | 3.5 | 3.7 |
| Jordan | 3.3 | 3.3 | 3.6 | ||
| Kazakhstan | 3.1 | 2.7 | |||
| Korea | 2.4 | 3.1 | 3.8 | 3.5 | 3.9 |
| Kyrgyzstan | 3.5 | 3.2 | |||
| Latvia | 5.3 | 3.7 | 3.7 | 3.0 | 2.4 |
| Liechtenstein | 4.1 | 3.6 | 3.9 | 2.8 | 4.1 |
| Lithuania | 3.0 | 2.4 | 2.5 | ||
| Luxembourg | 1.6 | 1.5 | 1.3 | 1.3 | 1.5 |
| Macao-China | 2.2 | 1.1 | 0.9 | 0.9 | |
| Macedonia | 1.9 | ||||
| Malaysia | 2.9 | 3.3 | |||
| Malta | 1.6 | ||||
| Massachusetts (USA) | 6.1 | ||||
| Mauritius | 1.1 | ||||
| Mexico | 3.3 | 4.1 | 3.1 | 2.0 | 1.5 |
| Miranda-Venezuela | 5.3 | ||||
| Montenegro | 1.2 | 1.7 | 1.2 | ||
| Netherlands | 3.4 | 2.9 | 2.9 | 5.1 | 3.5 |
| New Zealand | 2.8 | 2.5 | 3.0 | 2.4 | 2.4 |
| Norway | 2.8 | 2.8 | 3.2 | 2.6 | 3.2 |
| Panama | 6.5 | ||||
| Peru | 4.4 | 4.0 | 4.3 | ||
| Poland | 4.5 | 2.9 | 2.8 | 2.6 | 3.1 |
| Portugal | 4.5 | 3.7 | 3.6 | 3.1 | 3.8 |
| Qatar | 1.2 | 0.8 | 0.8 | ||
| Republic of Moldova | 2.8 | ||||
| Romania | 3.5 | 4.7 | 4.1 | 4.0 | |
| Russian Federation | 4.2 | 3.9 | 4.3 | 3.3 | 3.0 |
| Serbia | 3.5 | 2.4 | 3.4 | ||
| Shanghai-China | 2.4 | 2.9 | |||
| Singapore | 1.1 | 1.4 | |||
| Slovak Republic | 3.1 | 3.1 | 2.5 | 4.2 | |
| Slovenia | 1.0 | 1.0 | 1.2 | ||
| Spain | 2.7 | 2.6 | 2.2 | 2.0 | 1.9 |
| Sweden | 2.2 | 2.4 | 3.4 | 2.9 | 3.0 |
| Switzerland | 4.2 | 3.3 | 3.1 | 2.4 | 2.6 |
| Thailand | 3.2 | 2.8 | 2.6 | 2.6 | 3.1 |
| Trinidad and Tobago | 1.2 | ||||
| Tunisia | 2.8 | 4.0 | 2.9 | 4.5 | |
| Turkey | 5.8 | 4.2 | 3.5 | 4.2 | |
| United Arab Emirates | 2.9 | 2.5 | |||
| United Kingdom | 2.6 | 2.5 | 2.3 | 2.3 | 3.5 |
| United States | 7.0 | 3.2 | 3.7 | 3.7 | |
| Uruguay | 3.4 | 3.4 | 2.6 | 3.2 | |
| Yugoslavia | 3.6 |
Standardfehler Ländermittelwerte Mathematik
| country | se math 2000 | se math 2003 | se math 2006 | se math 2009 | se math 2012 |
|---|---|---|---|---|---|
| Albania | 3.1 | 4.0 | 2.0 | ||
| Argentina | 9.4 | 6.2 | 4.1 | 3.5 | |
| Australia | 3.5 | 2.1 | 2.2 | 2.5 | 1.6 |
| Austria | 2.7 | 3.3 | 3.7 | 2.7 | 2.7 |
| Azerbaijan | 2.3 | 2.8 | |||
| Belgium | 3.9 | 2.3 | 3.0 | 2.3 | 2.1 |
| Brazil | 3.7 | 4.8 | 2.9 | 2.4 | 1.9 |
| Bulgaria | 5.7 | 6.1 | 5.9 | 4.0 | |
| Canada | 1.4 | 1.8 | 2.0 | 1.6 | 1.8 |
| Chile | 3.7 | 4.6 | 3.1 | 3.1 | |
| Chinese Taipei | 4.1 | 3.4 | 3.3 | ||
| Colombia | 3.8 | 3.2 | 2.9 | ||
| Connecticut (USA) | 6.2 | ||||
| Costa Rica | 3.0 | 3.0 | |||
| Croatia | 2.4 | 3.1 | 3.5 | ||
| Czech Republic | 2.8 | 3.5 | 3.6 | 2.8 | 2.9 |
| Denmark | 2.4 | 2.7 | 2.6 | 2.6 | 2.3 |
| Estonia | 2.7 | 2.6 | 2.0 | ||
| Finland | 2.1 | 1.9 | 2.3 | 2.2 | 1.9 |
| Florida (USA) | 5.8 | ||||
| France | 2.7 | 2.5 | 3.2 | 3.1 | 2.5 |
| Georgia | 2.8 | ||||
| Germany | 2.5 | 3.3 | 3.9 | 2.9 | 2.9 |
| Greece | 5.6 | 3.9 | 3.0 | 3.9 | 2.5 |
| Hong Kong-China | 3.3 | 4.5 | 2.7 | 2.7 | 3.2 |
| Hungary | 4.0 | 2.8 | 2.9 | 3.5 | 3.2 |
| Iceland | 2.3 | 1.4 | 1.8 | 1.4 | 1.7 |
| India | 4.6 | ||||
| Indonesia | 4.5 | 3.9 | 5.6 | 3.7 | 4.0 |
| Ireland | 2.7 | 2.4 | 2.8 | 2.5 | 2.2 |
| Israel | 9.3 | 4.3 | 3.3 | 4.7 | |
| Italy | 2.9 | 3.1 | 2.3 | 1.9 | 2.0 |
| Japan | 5.5 | 4.0 | 3.3 | 3.3 | 3.6 |
| Jordan | 3.3 | 3.7 | 3.1 | ||
| Kazakhstan | 3.0 | 3.0 | |||
| Korea | 2.8 | 3.2 | 3.8 | 4.0 | 4.6 |
| Kyrgyzstan | 3.4 | 2.9 | |||
| Latvia | 4.5 | 3.7 | 3.0 | 3.1 | 2.8 |
| Liechtenstein | 7.0 | 4.1 | 4.2 | 4.1 | 4.0 |
| Lithuania | 2.9 | 2.6 | 2.6 | ||
| Luxembourg | 2.0 | 1.0 | 1.1 | 1.2 | 1.1 |
| Macao-China | 2.9 | 1.3 | 0.9 | 1.0 | |
| Macedonia | 2.7 | ||||
| Malaysia | 2.7 | 3.2 | |||
| Malta | 1.4 | ||||
| Massachusetts (USA) | 6.2 | ||||
| Mauritius | 1.0 | ||||
| Mexico | 3.4 | 3.6 | 2.9 | 1.8 | 1.4 |
| Miranda-Venezuela | 4.3 | ||||
| Montenegro | 1.4 | 2.0 | 1.1 | ||
| Netherlands | 3.6 | 3.1 | 2.6 | 4.7 | 3.5 |
| New Zealand | 3.1 | 2.3 | 2.4 | 2.3 | 2.2 |
| Norway | 2.8 | 2.4 | 2.6 | 2.4 | 2.7 |
| Panama | 5.2 | ||||
| Peru | 4.4 | 4.0 | 3.7 | ||
| Poland | 5.5 | 2.5 | 2.4 | 2.8 | 3.6 |
| Portugal | 4.1 | 3.4 | 3.1 | 2.9 | 3.8 |
| Qatar | 1.0 | 0.7 | 0.8 | ||
| Republic of Moldova | 3.1 | ||||
| Romania | 4.3 | 4.2 | 3.4 | 3.8 | |
| Russian Federation | 5.5 | 4.2 | 3.9 | 3.3 | 3.0 |
| Serbia | 3.5 | 2.9 | 3.4 | ||
| Shanghai-China | 2.8 | 3.3 | |||
| Singapore | 1.4 | 1.3 | |||
| Slovak Republic | 3.3 | 2.8 | 3.1 | 3.4 | |
| Slovenia | 1.0 | 1.2 | 1.2 | ||
| Spain | 3.1 | 2.4 | 2.3 | 2.1 | 1.9 |
| Sweden | 2.5 | 2.6 | 2.4 | 2.9 | 2.3 |
| Switzerland | 4.4 | 3.4 | 3.2 | 3.3 | 3.0 |
| Thailand | 3.6 | 3.0 | 2.3 | 3.2 | 3.4 |
| Trinidad and Tobago | 1.3 | ||||
| Tunisia | 2.5 | 4.0 | 3.0 | 3.9 | |
| Turkey | 6.7 | 4.9 | 4.4 | 4.8 | |
| United Arab Emirates | 2.5 | 2.4 | |||
| United Kingdom | 2.5 | 2.4 | 2.1 | 2.4 | 3.3 |
| United States | 7.6 | 2.9 | 4.0 | 3.6 | 3.6 |
| Uruguay | 3.3 | 2.6 | 2.6 | 2.8 | |
| Yugoslavia | 3.8 |
Standardfehler Ländermittelwerte Naturwissenschaften
| country | se scie 2000 | se scie 2003 | se scie 2006 | se scie 2009 | se scie 2012 |
|---|---|---|---|---|---|
| Albania | 2.9 | 4.0 | 2.0 | ||
| Argentina | 8.6 | 6.2 | 4.1 | 3.5 | |
| Australia | 3.5 | 2.1 | 2.2 | 2.5 | 1.6 |
| Austria | 2.7 | 3.3 | 3.7 | 2.7 | 2.7 |
| Azerbaijan | 2.3 | 2.8 | |||
| Belgium | 4.3 | 2.3 | 3.0 | 2.3 | 2.1 |
| Brazil | 3.3 | 4.8 | 2.9 | 2.4 | 1.9 |
| Bulgaria | 4.6 | 6.1 | 5.9 | 4.0 | |
| Canada | 1.6 | 1.8 | 2.0 | 1.6 | 1.8 |
| Chile | 3.4 | 4.6 | 3.1 | 3.1 | |
| Chinese Taipei | 4.1 | 3.4 | 3.3 | ||
| Colombia | 3.8 | 3.2 | 2.9 | ||
| Connecticut (USA) | 6.2 | ||||
| Costa Rica | 3.0 | 3.0 | |||
| Croatia | 2.4 | 3.1 | 3.5 | ||
| Czech Republic | 2.4 | 3.5 | 3.6 | 2.8 | 2.9 |
| Denmark | 2.8 | 2.7 | 2.6 | 2.6 | 2.3 |
| Estonia | 2.7 | 2.6 | 2.0 | ||
| Finland | 2.5 | 1.9 | 2.3 | 2.2 | 1.9 |
| Florida (USA) | 5.8 | ||||
| France | 3.2 | 2.5 | 3.2 | 3.1 | 2.5 |
| Georgia | 2.8 | ||||
| Germany | 2.4 | 3.3 | 3.9 | 2.9 | 2.9 |
| Greece | 4.9 | 3.9 | 3.0 | 3.9 | 2.5 |
| Hong Kong-China | 3.0 | 4.5 | 2.7 | 2.7 | 3.2 |
| Hungary | 4.2 | 2.8 | 2.9 | 3.5 | 3.2 |
| Iceland | 2.2 | 1.4 | 1.8 | 1.4 | 1.7 |
| India | 4.6 | ||||
| Indonesia | 3.9 | 3.9 | 5.6 | 3.7 | 4.0 |
| Ireland | 3.2 | 2.4 | 2.8 | 2.5 | 2.2 |
| Israel | 9.0 | 4.3 | 3.3 | 4.7 | |
| Italy | 3.1 | 3.1 | 2.3 | 1.9 | 2.0 |
| Japan | 5.5 | 4.0 | 3.3 | 3.3 | 3.6 |
| Jordan | 3.3 | 3.7 | 3.1 | ||
| Kazakhstan | 3.0 | 3.0 | |||
| Korea | 2.7 | 3.2 | 3.8 | 4.0 | 4.6 |
| Kyrgyzstan | 3.4 | 2.9 | |||
| Latvia | 5.6 | 3.7 | 3.0 | 3.1 | 2.8 |
| Liechtenstein | 7.1 | 4.1 | 4.2 | 4.1 | 4.0 |
| Lithuania | 2.9 | 2.6 | 2.6 | ||
| Luxembourg | 2.3 | 1.0 | 1.1 | 1.2 | 1.1 |
| Macao-China | 2.9 | 1.3 | 0.9 | 1.0 | |
| Macedonia | 2.1 | ||||
| Malaysia | 2.7 | 3.2 | |||
| Malta | 1.4 | ||||
| Massachusetts (USA) | 6.2 | ||||
| Mauritius | 1.0 | ||||
| Mexico | 3.2 | 3.6 | 2.9 | 1.8 | 1.4 |
| Miranda-Venezuela | 4.3 | ||||
| Montenegro | 1.4 | 2.0 | 1.1 | ||
| Netherlands | 4.0 | 3.1 | 2.6 | 4.7 | 3.5 |
| New Zealand | 2.4 | 2.3 | 2.4 | 2.3 | 2.2 |
| Norway | 2.7 | 2.4 | 2.6 | 2.4 | 2.7 |
| Panama | 5.2 | ||||
| Peru | 4.0 | 4.0 | 3.7 | ||
| Poland | 5.1 | 2.5 | 2.4 | 2.8 | 3.6 |
| Portugal | 4.0 | 3.4 | 3.1 | 2.9 | 3.8 |
| Qatar | 1.0 | 0.7 | 0.8 | ||
| Republic of Moldova | 3.1 | ||||
| Romania | 3.4 | 4.2 | 3.4 | 3.8 | |
| Russian Federation | 4.7 | 4.2 | 3.9 | 3.3 | 3.0 |
| Serbia | 3.5 | 2.9 | 3.4 | ||
| Shanghai-China | 2.8 | 3.3 | |||
| Singapore | 1.4 | 1.3 | |||
| Slovak Republic | 3.3 | 2.8 | 3.1 | 3.4 | |
| Slovenia | 1.0 | 1.2 | 1.2 | ||
| Spain | 3.0 | 2.4 | 2.3 | 2.1 | 1.9 |
| Sweden | 2.5 | 2.6 | 2.4 | 2.9 | 2.3 |
| Switzerland | 4.4 | 3.4 | 3.2 | 3.3 | 3.0 |
| Thailand | 3.1 | 3.0 | 2.3 | 3.2 | 3.4 |
| Trinidad and Tobago | 1.3 | ||||
| Tunisia | 2.5 | 4.0 | 3.0 | 3.9 | |
| Turkey | 6.7 | 4.9 | 4.4 | 4.8 | |
| United Arab Emirates | 2.5 | 2.4 | |||
| United Kingdom | 2.7 | 2.4 | 2.1 | 2.4 | 3.3 |
| United States | 7.3 | 2.9 | 4.0 | 3.6 | 3.6 |
| Uruguay | 3.3 | 2.6 | 2.6 | 2.8 | |
| Yugoslavia | 3.8 |
Wählerstromanalyse Gemeinderatswahl Salzburg 2014
Diese Wählerstromanalyse berechnet alle Anteile an den Wahlberechtigten. Erst dann wird die wahre Dimension der Verschiebungen bei den Wählern sichtbar.
Wir berücksichtigen in der Analyse alle Parteien, die bei einer der beiden Wahlen mindestens 1000 Stimmen (etwa 1% der Wahlberechtigten) erreichen konnten.
Alle übrigen Stimmen, also ungültige Stimmen und Stimmen für Kleinstparteien, und die Nichtwähler, fassen wir unter der Bezeichnung NW zusammen.
Ausgangslage (Gemeinderatswahl 2009, Anteile an Wahlberechtigten) waren folgende Parteienanteile
| SPÖ | ÖVP | BL | FPÖ | KPÖ | TAZL | NW |
|---|---|---|---|---|---|---|
| 18.3 | 13.5 | 8.1 | 7.0 | 1.0 | 2.4 | 49.7 |
Das neue Wahlergebnis (Gemeinderatswahl 2014, Anteile an Wahlberechtigten) zeigt folgende Parteienanteile
| SPÖ | ÖVP | GRÜNE | FPÖ | KPÖ | NEOS | SALZ | NW |
|---|---|---|---|---|---|---|---|
| 13.7 | 8.1 | 5.7 | 5.5 | 0.9 | 5.1 | 1.4 | 59.5 |
Das wohl dramatischste Ergebnis der Wahl ist, dass 2014 knapp 60 Prozent der Wähler keiner der angeführten Parteien ihre Stimme gegeben habe. Der entsprechende Anteil lag 2009 bei knapp unter 50%.
Wie viele Stimmen sind zwischen 2009 und 2014 zwischen den Parteien gewandert?
| SPÖ | ÖVP | GRÜNE | FPÖ | KPÖ | NEOS | SALZ | NW | Schw | |
|---|---|---|---|---|---|---|---|---|---|
| SPÖ | 12500 | 0 | 0 | 200 | 0 | 0 | 0 | 7500 | 1400 |
| ÖVP | 200 | 8400 | 900 | 100 | 0 | 3100 | 800 | 1600 | 1200 |
| BL | 0 | 0 | 5000 | 0 | 500 | 2600 | 800 | 0 | 1200 |
| FPÖ | 2300 | 0 | 0 | 4800 | 0 | 0 | 0 | 600 | 1400 |
| KPÖ | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 1100 | 800 |
| TAZL | 200 | 600 | 300 | 1000 | 200 | 0 | 0 | 200 | 1100 |
| NW | 0 | 0 | 0 | 0 | 200 | 0 | 0 | 54800 | 1400 |
Aus der zweiten Zeile kann man ablesen, dass etwa 900 ÖVP-Wähler von 2009 2014 die Grünen und etwa 3100 die NEOS gewählt haben.
Die mit Schw bezeichnete Spalte gibt die Schwankungsbreite der geschätzten Wählerströme für jede Zeile an.
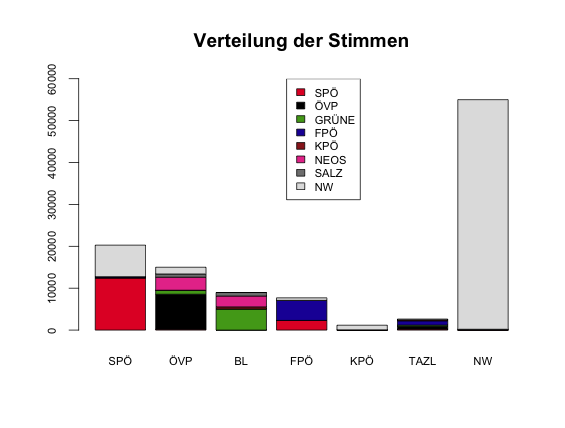
Die nächste Grafik zeigt, welchen Anteil ihrer Wähler von 2009 die Parteien 2014 an welche Parteien verloren haben.
| SPÖ | ÖVP | GRÜNE | FPÖ | KPÖ | NEOS | SALZ | NW | Schw | |
|---|---|---|---|---|---|---|---|---|---|
| SPÖ | 61.5 | 0.0 | 0.0 | 1.2 | 0.1 | 0.0 | 0.0 | 37.2 | 7.0 |
| ÖVP | 1.3 | 55.8 | 6.0 | 0.4 | 0.0 | 20.7 | 5.1 | 10.7 | 7.8 |
| BL | 0.0 | 0.0 | 56.2 | 0.0 | 5.6 | 28.9 | 9.3 | 0.0 | 13.6 |
| FPÖ | 30.0 | 00.0 | 0.0 | 62.2 | 0.0 | 0.0 | 0.0 | 7.9 | 18.1 |
| KPÖ | 0.0 | 0.0 | 0.0 | 0.0 | 4.4 | 0.0 | 0.0 | 95.6 | 67.1 |
| TAZL | 8.2 | 24.1 | 12.8 | 38.8 | 9.5 | 0.0 | 0.0 | 6.5 | 42.9 |
| NW | 00.0 | 0.0 | 0.0 | 0.0 | 0.4 | 0.0 | 0.0 | 99.6 | 2.6 |
Aus der zweiten Zeile kann man ablesen, dass etwa 6% der ÖVP-Wähler von 2009 2014 die Grünen und etwa 20% die NEOS gewählt haben.
Außerdem fällt auf, dass SPÖ und FPÖ nur etwas mehr als 60% ihrer Wähler halten konnten. Bei ÖVP und Grünen war die Haltequote noch geringer, sie lag nur bei etwa 55%.
Die folgende Grafik zeigt, wie sich die Wähler der Parteien von 2009 bei der Wahl von 2014 entschieden haben:
Die Grafik zeigt ganz deutlich, dass sowohl die ÖVP als auch die Grünen erheblich an die NEOS verloren haben.
Die SPÖ hat vor allem an die Nichtwähler verloren.
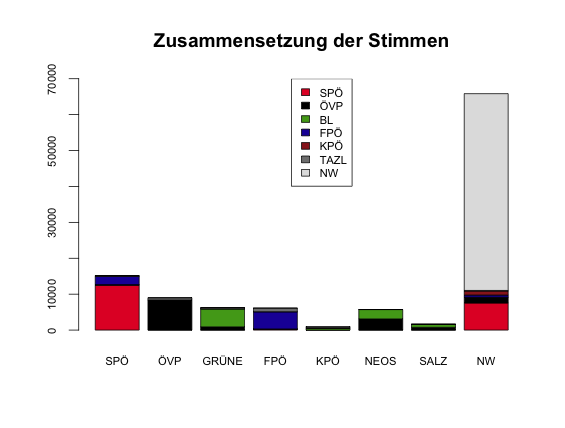
Schließlich sehen wir uns noch an, woher die Stimmen der Parteien 2014 gekommen sind:
Die SPÖ konnte also Stimmen von der FPÖ gewinnen. Weitaus mehr frühere SPÖ-Wähler findet man aber 2014 unter den Nichtwählern. Die NEOS konnten ihre Stimmen vor allem von der ÖVP und von den Grünen gewinnen.
Methodisches zur Wählerstromanalyse findet man in einem früheren Blog-Artikel. Bie der vorliegenden Analyse wurden ca. 160 Sprengelergebnisse aus der Stadt Salzburg verwendet.
PISA, Bildung und Bildungsstandards
PISA 2015 wird also in Österreich abgesagt.
Manche sind froh darüber, manche nicht.
Die Gegner standardisierter Tests (und dazu gehören viele AHS-Lehrer_innen) meinen immer, dass man sich bei standardisierten Tests nach unten orientieren muss und daher ein allgemeiner Niveauverlust die Folge ist. Aus der Sicht der einzelnen Lehrer_innen kann das durchaus richtig sein. Man kann als guter Lehrer einige Fragen, die einem persönlich sehr am Herzen liegen, vertiefend behandeln und dann auch entsprechend schwerere Prüfungsfragen stellen.
Das funktioniert aber nur, weil Lehrer und Prüfer die selbe Person sind. Und es führt dazu, dass das, was als höheres Niveau angesehen wird, von Schule zu Schule sehr verschieden sein kann.
Das, was an allen Schulen als unbedingt zu erreichender Mindeststandard über alle Gebiete und Themen hinweg angesehen wird, ist auch heute schon von Schule zu Schule sehr verschieden.
Als Universitätslehrer merke ich das ganz deutlich. Ich kann kaum einen Inhalt oder eine Fertigkeit, die eigentlich im AHS-Lehrplan als verbindlich niedergeschrieben ist, bei allen meinen Studierenden voraussetzen.
Auch wenn etwas im Lehrplan steht und sogar vielleicht unterrichtet wird, kann Lehrer_in Gebiete, bei denen es mit der Vermittlung nicht ganz so klappt, bei der Prüfung weglassen und daher fallen dann Mängel bei der Abdeckung mancher Inhalte nicht auf.
Die Testkultur wie bei PISA und bei der Zentralmatura führt dazu, dass sich das Bildungssystem daran gewöhnt, dass die Überprüfung der Fähigkeiten nicht von den Vermittlern selbst, sondern von externen Institutionen gesteuert wird.
Das ist natürlich ein Eingriff in die Autonomie der einzelnen Schulen. Und eine Einschränkung der Autonomie der Lehrer_innen bei der Schwerpunktsetzung.
Die große Gefahr bei standardisierten Tests ist natürlich, dass der Unterricht sich nahezu ausschließlich an den standardisierten Tests orientiert. Das muss aber nicht sein. Denkbar ist, dass die verbindlichen standardisierten Lernziele und Kompetenzen so festgelegt werden, dass sie in etwas weniger als 50% der Unterrichtszeit ausreichend vermittelt werden können. Dann bleibt immer noch mehr als die Hälfte der Zeit für vertiefenden standortspezifische Inhalte!
Dass wir zwar eine Zentralmatura haben, die Beurteilung der zentral vorgegebenen Prüfung dann aber doch vor allem durch die Lehrer geschieht, die die Schüler auf die Prüfung vorbereitet haben, läuft übrigens dem Ziel der Standardisierung und Vergleichbarkeit zuwider. Ohne besonderen Mehraufwand für die Lehrer_innen könne man ihnen ja auch die Prüfungsarbeiten aus anderen Schulen „zuteilen“.
Über die starken „Kompetenzschwankungen“ von Studierenden kann ich einiges an Erfahrung beisteuern.
Ich halte unter anderem Lehrveranstaltungen zur Fachdidaktik der Informatik für Lehramtskandidaten an der Universität Wien. Alle Lehramtskandidaten brauchen ja noch ein zweites Unterrichtsfach. Und da ist der Strauß bei meinen Informatik-Studierenden besonders breit gefächert. Bei meinen Studierenden findet man als „das andere Fach“ so ziemliche alles denkbare: Mathematik, Physik, Chemie, Sport, Geschichte, Germanistik, Anglistik, Französisch, Religion, Geografie, Musik, …
Informatik kann man nicht ganz ohne mathematisches Grundwissen betreiben. Zum didaktischen Umgehen mit Computergrafik braucht man elementares Grundwissen über Winkelfunktionen. Das ist Stoff des AHS-Lehrplans der 9. Schulstufe. Es gibt jedes Jahr einige Studierende, denen ich diese Grundbegriffe in einem Schnellsiederkurs nahebringen muss. Da wäre ein Bildungsstandard, bei dem ich davon ausgehen kann, dass alle Studierenden in meinen Lehrveranstaltungen darüber Bescheid wissen, schon sehr recht. Und ich meine auch, dass Winkelfunktionen ein Teil der Allgemeinbildung sind, und dass daher meine Studierenden mit österreichischer Matura, die ja die allgemeine Studierfähigkeit bescheinigen soll, darüber Bescheid wissen sollte. Und zwar alle, nicht nur die mit einem Zweitfach Mathematik oder mit naturwissenschaftlicher Ausrichtung. Informatik-Lehramts-Studenten sollten das als Teil ihrer Allgemeinbildung wissen. Zu viele wissen es aber nicht.
Wenn jeder Maturant bei der Matura damit rechnen muss, dass alles, was im verbindlichen Katalog steht, auch tatsächlich zur Prüfung kommen kann, dann besteht eine Chance, dass mehr Studierende als bisher darüber Bescheid wissen.
PISA-Absage und die Folgen
Bei PISA einmal nicht mitzutun hat auch einige vielleicht nicht ausreichend bedachte Auswirkungen.
PISA läuft in einem Dreierzyklus ab.
Bei jedem Test ist eines der 3 Gebiete Lesen – Mathematik – Naturwissenschaften Schwerpunktgebiet. 2015 sind die Naturwissenschaften das Schwerpunktgebiet. Da wird der Aufgabenkatalog für Naturwissenschaften neu erarbeitet. Dazu dienen auch die jetzt abgesagten Vortests. Die Ergebnisse der Vortests der einzelnen Länder helfen dabei, den Test international vergleichbar zu gestalten. In den beiden folgenden Testzyklen (2018 und 2021) werden dann einfach Aufgaben von 2015 weiterverwendet. Wenn wir also 2015 nicht teilnehmen, dann ist der Naturwissenschaftstest für 2018 und 2021 auch nicht unter Einbeziehung Österreichs geeicht und kann daher auch nicht die selbe Aussagekraft wir für andere Länder haben.
Außerdem erscheint es mir peinlich, wenn Österreich als erstes OECD-Mitgliedsland aus dem Test aussteigt. Zu unserem internationalen Ansehen wird das nicht beitragen.
Bildungsstandards und Zentralmatura für ein Jahr auszusetzen ist zwar unerfreulich und im Falle der Zentralmatura für die betroffenen Schüler wohl auch eine Zumutung.
Aber bei PISA 2015 auszusteigen hat negative Folgewirkungen, die wir erst 2024 wieder bereinigen können. Bis dahin sind unsere PISA-Werte nicht unter den selben Bedingungen erhoben wie die der anderen teilnehmenden OECD-Mitgliedsländer.
Vom schlampigen Umgang mit Meinungsumfragen
Ich musste bei diesem Eintrag etwas korrigieren!
Im aktuellen profil gibts einen Artikel zum Thema Umfrage zur Adoption durch Homosexuelle.
Da gehts darum, dass laut einer Umfrage 53% der Befragten dafür sind, dass Homosexuelle Kinder adoptieren dürfen.
In dem kurzen Artikel steht nichts über die Anzahl der Befragten, und es gibt auch keine Informationen zur statistischen Schwankungsbreite.
Vielleicht hab ich das beim ersten mal Lesen übersehen, oder aber es ist gestern noch nicht dort gestanden, jetzt steht jedenfalls dort, dass 500 Personen befragt wurden.
Die fehlenden Angaben zur Schwankungsbreite sind in diesem Fall ziemlich ärgerlich, weil es ja darum geht, ob man sagen kann, dass es statistisch einigermaßen gesichert ist, dass die Mehrheit der Österreicher (nicht der nur der Befragten) diese Meinung hat.
Wenn man 500 Personen befragt hat, dann gibt es bei diesem Anteil einen Schwankungsbereich vom 48,6% bis 57,4%. Da müssen aber alle Befragten eine auswertbare Antwort gegeben haben. Hat doch eine merkbarer Anteil der Befragten keine zuordenbare Antwort gegeben, dann ist der Schwankungsbereich noch größer. Man kann also nicht sagen, dass die Umfrage statistisch gesichert den Schluss zulässt, dass die Mehrheit der Österreicher dafür ist, auch Homosexuellen die Adoption von Kindern zu ermöglichen.
Statistisch sauber wäre es, zu sagen, dass diese Umfrage zeigt, dass das ein Thema ist, das auf der Kippe steht. Eine Mehrheit dafür liegt im Bereich des Möglichen, statistisch gesichert ist sie aber nicht.
Vielleicht sollten profil-Mitarbeiter doch meinen Blog-Eintrag über die Aussagekraft von Meinungsumfragen lesen.