Die Menschheit im Bodensee
In meinem täglichen Mathematik-Puzzle (#mathepuzzle von @neuwirthe auf Twitter) habe ich heute folgende Aufgabe gestellt:
Wenn die gesamte Menschheit im Bodensee untertaucht, um wieviel steigt dann der Wasserspiegel.
Natürlich gibt es da keine genaue Antwort, es geht um die Größenordnung: cm, mm, dm, m, 10m, 100m, km …?
Welche Informationen braucht man denn, um diese Überschlagsrechnung anzustellen? Man braucht das Volumen der Menschheit und die Fläche des Bodensees.
Ja, die Fläche, nicht das Volumen des Sees!
Warum nur die Fläche? Stellen wir uns vor, wir wollen die Menschheit auf dem zugefrorenen Bodensee aufstellen? Geht sich das aus?
In der Vor-Wikipedia-Zeit konnte man mit einer Landkarte feststellen, dass der Bodensee eine Fläche von ungefähr 500 km² bedeckt. Heutzutage kann man einfach in der Wikipedia nachschlagen. Das sind 500 Millionen m² oder 0.5 Milliarden m². Laut Schätzungen gibt es derzeit knapp 8 Milliarden Menschen. Wenn wir also 16 Menschen auf 1 m² unterbringen, dann können wir alle Menschen auf dem zugefrorenen Bodensee aufstellen. Die Menschenschicht auf dem Bodensee, die den Bodensee bedeckt, ist dann ca. 1.50 m hoch.
Es spielt dabei keine Rolle, wie tief der Bodensee ist, oder, anders gesagt, das Volumen des Sees spielt keine Rolle.
Wir können auch etwas anders rechnen.
Wie groß ist eigentlich das Volumen eines Menschen? Wir wissen, dass Menschen hauptsächlich aus Wasser bestehen und daher ziemlich das selbe spezifische Gewicht haben. Man kann das auch empirisch überprüfen. Wenn man im Schwimmbad einatmet, dann treibt man auf dem Wasser, wenn man komplett ausatmet, dann geht man (fast) unter. Auch das belegt, dass das spezifische Gewicht eines Menschen ziemlich gleich mit dem spezifischen Gewicht von Wasser ist.
Wenn wir von einem Durchschnittsgewicht eines Menschen vom 75 kg ausgehen, dann hat ein Mensch also ein Volumen von 75 dm³. Vereinfachend können wir also sagen, dass 15 Menschen ungefähr ein Volumen von 1.1 m³ haben. Das Volumen der gesamten Menschheit ist daher 1.1﹒(8﹒10⁹)/15 ≈ 0.6﹒10⁹ und das ergibt auf einer Fläche von 0.5﹒10⁹ m² verteilt eine Höhe von 1.2 m.
Wenn die Menschheit jetzt untertaucht, dann verdrängt sie genau ihr eigenes Volumen an Wasser und der Wasserspiegel steigt um die berechnete Höhe.
Der Wasserspiegel würde also um ungefähr 1 m steigen.
Nachtrag zur 130-vs-140 km/h-Rechnung
Im gestrigen Blogeintrag habe ich als Hilfsmittel Excel verwendet.
Es muss nicht unbedingt Excel sein, mit anderen Tabellenkalulationsprogrammen (LibreOffice, GoogleSheets, …) gehts auch.
Ich habe auch geschrieben, dass ich das Beispiel für schulgeeignet halte, allerdings nur mit Tabellenkalkulation.
Ich möchte heute zeigen, wie man das Beispiel in „klassischer“ Art mit algebraischen Formeln rechnen müsste.
Noch einmal das Problem:
Zwei Autos, das langsamere mit Geschwindigkeit $V_1$, das schnellere mit Geschwindigkeit $V_2$, merken an der selben Stelle, dass sie bremsen müssen. Welche Geschwindigkeit hat das schnellere an der Stelle, an der das langsamere stehen bleibt.
Wir starten mit Parametern:
$V_1$ und $V_2$ ist die Geschwindigkeiten.
Die Reaktionszeit ist $t_0$.
Die Bremsverzögerung ist $a$.
Wir nehmen an, dass Bremsverzögerung und Reaktionszeit für beide Fahrer und beide Autos gleich sind.
Dann ist die Geschwindigkeit des langsameren Autos zum Zeitpunkt $t$ (0 ist der Zeitpunkt, an dem die Fahrer merken, dass sie bremsen müssen)
$v_1(t)=V_1- a (t-t_0)$
Genau genommen gilt die Formel nur solange, bis die Geschwindigkeit 0 beträgt.
Analog gilt natürlich für das schneller Auto
$v_2(t)=V_2 – a (t-t_0)$
Die Strecken, die die beiden Autos biz zum Zeitpunkt $t$ zurückgelegt haben, sind
$s_1(t)=V_1 t – \frac{a(t-t_0)^2}{2}$
$s_2(t)=V_2 t – \frac{a(t-t_0)^2}{2}$
Der lineare Term in diesen Formeln ist der Reaktionsweg, der quadratische der Bremsweg, die Summe heißt Anhalteweg.
Diese Formeln gelten nur nach Ablauf der Reaktionszeit und bis zum Stillstand des Autos.
Wann kommt das langsamere Auto zum Stillstand, und welche Strecke hat es bis dahin zurückgelegt?
Anders gefragt: Für welches $t=t_1$ gilt $v_1(t_1)=0$ und wie lang ist dann der Anhalteweg.
Wir lösen dazu
$V_1-a (t-t_0)=0$.
Die Lösung ist $t_1=t_0+\frac{V_1}{a}$
Der Anhalteweg ist daher
$b_1=s_1(t_1)=V_1 t_0 + \frac{V_1^2}{2 a}$
Wann erreicht das schnellere Auto den Anhaltepunkt des langsameren?
Dazu müssen wir folgende Gleichung (für $t$) lösen:
$s_2(t)=b_1$ oder ausgeschrieben
$V_2 t – \frac{a(t-t_0)^2}{2}=V_1 t_0 + \frac{V_1^2}{2 a}$
Das ist nicht mehr ganz einfach, aber da es sich um eine quadratische Gleichung handelt ist es möglich. Wir erhalten 2 Lösungen:
$t_2= t_0 + \frac{V_2}{a} – \frac{\sqrt{(v_2-v_1)(2 a t_0 + v_1 + v_2)}}{a}$
und
$t_2= t_0 + \frac{V_2}{a} + \frac{\sqrt{(v_2-v_1)(2 a t_0 + v_1 + v_2)}}{a}$
Welche der beiden Lösung passt zu unserem Problem? Analog zur Rechnung für das langsamere Auto sehen wir, dass das schnelle Auto zum Zeitpunkt $t_0 + \frac{V_2}{a}$ stehen bleibt.
Der zweite „Lösungszeitpunkt“ liegt also nach dem Zeitpunkt, wo auch das schnellere Auto bereits steht, daher können wir nur die erste Lösung verwenden.
Jetzt müssen wir nur noch den Zeitpunkt $t_2$ in die Geschwindigkeitsformel $v_2(t)$ für $t$ einsetzen, dann haben wir die Aufprallgeschwindigkeit.
$v_2(t_2)=\sqrt{(V_2-V_1)(2 a t_0 +V_1 + V_2)}$
All diese Formeln und Gleichungen gehen davon aus, dass wir in einem einheitlichen Maßsystem, also Metern (m) und Sekunden (s) rechnen. Für praktische Zwecke wollen wir aber die Geschwindigkeiten in km/h angeben. Wir müssen dazu als Geschwindigkeiten von km/h in m/s umrechnen.
Da eine Stunde 3600 Sekunden hat sind 1 m/s = 3600 m/h = 3,6 km/h und umgekehrt natürlich
1 km/h = 1/3,6 m/s.
Wenn wir jetzt die Reaktionszeit $t_0$ = 0,8 s, die Bremsverzögerung
$a$ = 7,5 m/s$^2$, $V_1$=130 km/h = 36,11 m/s und $V_2$=140 km/h = 38,89 m/s in unsere Formel einsetzen, dann ergibt das eine Aufprallgeschwindigkeit von
$v_2(t_2)$ = 15,55 m/s = 55,99 km/h
Diese Art der Darstellung ist in gewissem Sinn als abschreckendes Beispiel gedacht.
Die Umformungen sind „denkaufwendig“ und das Gleichungslösen und Termeinsetzen einfach mühselig.
Die Berechnung mit Tabellenkalkulation erscheint mir wesentlich einfacher und didaktisch weitaus ergiebiger.
Man hat beim Rechnen mit der Tabellenkalkulation auch immer Zahlen vor Augen, und bei diesen Zahlen hat man auch während des Modelliervorgangs eine Vorstellung über die Qualität der Lösung. Modellfehler entdeckt man in der Regel früher, weil man sehen kann, ob die Zahlen mit der Vorstellung von der Lösung einigermaßen zusammenpassen.
130 km/h oder 140 km/h – Was ist der Unterschied beim Bremsen?
Der Minister für Verkehr, Innovation und Technologie überlegt, die Höchstgeschwindigkeit auf Autobahnen von 130 km/h auf 140 km/h zu erhöhen.
Ein Tweet des VCÖ (Verkehrsclub Österreich) hat mich auf die Idee gebracht, dazu ein paar Rechnungen anzustellen.
Wie wirkt sich denn die höhere Geschwindigkeit auf den Bremsweg aus?
Dazu brauchen wir ein paar weitere Zahlen.
Wir gehen von einer Reaktionszeit vom 0.8 Sekunden aus (das ist eine „gute“ Reaktion, man findet Angaben von 1 Sekunde oder mehr).
Während der Reaktionszeit verringert sich die Geschwindigkeit nicht, die ersten 0.8 Sekunden lang fährt das Auto mit 130 km/h.
Die Bremsverzögerung wird in m/s^2 angegeben und ein realistischer Wert auf trockener Straße und mit guten Bremsen ist 7.5 m/s^2. Das bedeutet, dass die Geschwindigkeit pro Sekunde um 7.5 m/s abnimmt. Wir müssen also die Anfangsgeschwindigkeit von 130 km/h in m/s umrechnen. Eine Stunde hat 60*60=3600 Sekunden, in einer Stunde legt also ein Auto mit 1 m/s 3600 m oder 3.6 km zurück.
Geschwindigkeiten in m/s rechnet man also in km/h um, indem man sie mit 3.6 multipliziert und umgekehrt rechnet man km/h in m/s um, indem man durch 3.6 dividiert. Also sind 130 km/h (gerundet) 36.1 m/s.
Wir können die Geschwindigkeit unseres Autos zu jedem Zeitpunkt also auch in m/s ausrechnen. Das geschieht in dieser Excel-Tabelle.
Diese Excel-Tabelle verwendet nicht die Formeln, mit denen solche Probleme im Mathematikunterricht üblicherweise behandelt werden! Wir machen es einfacher.
In dieser Tabelle berechnen wir Geschwindigkeit und Fahrweg des Autos in einer Tabelle mit einem Zeitraster von Zehntelsekunden (Spalte mit der Überschrift t).
Wir wissen, dass die Geschwindigkeit bis zum Zeitpunkt 0.8 Sekunden 36.1 m/s beträgt. Danach nimmt sie pro Zehntelsekunde um 0.75 m/s ab. Die entsprechenden Werte stehen in der Tabelle in der Spalte mit dem Titel v(t) m/s.
Den Fahrweg können wir auch durch Aufaddieren der einzelnen Wegstrecken berechnen. Wir kennen ja die Geschwindigkeit zu den einzelnen Zeitpunkten. Den zurückgelegten Fahrweg von Sekunde 1.3 bis Sekunde 1.4 können wir berechnen, indem wir die mittlere Geschwindigkeit in diesem Zeitraum berechnen
(also den Mittelwert der Geschwindigkeit bei 1.3 s und bei 1.4 s) und mit der Zeit 0.1 s multiplizieren. Diese Werte stehen in der Spalte s(t) m. Da wir Geschwindigkeiten auch in km/h angeben wollen, gibt es noch die entsprechende Spalte, in der natürlich nur die Geschwindigkeit in m/s mit 3.6 multipliziert wird.
Das Auto mit 130 km/h kommt also nach 5.6 Sekunden und 116 m Bremsweg zum Stillstand.
In den Spalten daneben rechnen wir das gleiche für eine Geschwindigkeit von 140 km/h.
Die Bremszeit beträgt da 6 Sekunden und der Bremsweg 140 m. Der Unterschied ist anscheinend nicht gewaltig.
Wie schaut die Sache aber aus, wenn (der|die) Fahrer(in)? ein Hindernis gerade 116 m vorher erkannt hätte? Das Auto mit 130 km/h hätte gerade rechtzeitig gebremst. Das Auto mit 140 km/h wäre auf das Hindernis aufgefahren. Wichtige Frage: Mit welcher Geschwindigkeit wäre es aufgefahren?
Das können wir feststellen, wenn wir in der Tabelle für das Auto mit 140 km/h schauen, welche Geschwindigkeit das Auto bei einer Strecke von 116 m hat. Es sind ungefähr 56 km/h!
Wenn das schnellere Auto statt mit 140 kmh mit 160 km/h führe, dann hätte es nach 116 m eine Geschwindigkeit vom 100 km/h.
Um das herauszufinden muss man nur die Zahl 140 (in der grünen Zelle in der Tabelle) ändern und dann in der „Wegspalte“ den Wert von 116 m (oder nahe dran) suchen.
Didaktische Zusatzbemerkungen:
Für diese Art von Rechnung gibt es keine einfach handhabbaren „klassischen“ Formeln. Ein paar grundsätzliche Überlegungen und etwas Verständnis dafür, wie Zeit, Weg und Geschwindigkeit zusammenhängen erlauben es aber, die Tabelle aufzustellen, und mit dieser Tabelle kann man dann auch die „Aufschlaggeschwindigkeit“ des schnelleren Autos berechnen.
Wenn man die Geschwindigkeiten ändert, dann kann man beispielsweise auch berechnen, welche Geschwindigkeit ein Auto mit 130 km/h nach der Strecke hat, bei der ein Auto mit 100 km/h schon zum Stillstand gekommen ist.
Wenn man also Tabellenkalkulation sinnvoll einsetzt, dann kann man etwas berechnen, das ein Betrag des Mathematikunterrichts zur politischen Bildung sein kann.
Der Dominobogen
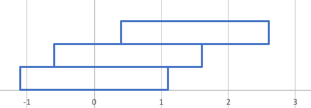
Wenn wir einen Dominostein seitlich verschoben auf einen anderen legen, dann können wir ihn fast um die halbe Länge nach rechts verschieben und er wird liegenbleiben und nicht herunterfallen.
Wenn wir noch einen weiteren (dritten) Stein drauflegen und wieder um fast die halbe Steinlänge verschieben, dann ist der schiefe Turm nicht mehr stabil und stürzt ein. Der Grund ist physikalisch. Der Schwerpunkt der beiden oberen Steine gemeinsam liegt nicht mehr innerhalb der Grundfläche des unteren Steins.
In unserem Fall sind die Steine alle 2.2 Einheiten lang. Der Schwerpunkt des untersten Steins liegt bei 0, der des mittleren Steins bei 1 und der des obersten Steins bei 2. Der mittlere und der obere Stein gemeinsam haben den Schwerpunkt bei 1.5 und das liegt außerhalb des rechtesten Punkts des untersten Steins (1.1). Der Turm knickt deshalb zwischen dem untersten und dem mittleren Stein ein.
Wie weit können wir denn den obersten Stein verschieben und doch noch einen stabilen Turm bekommen?
Da der 2. Stein den Spielraum schon fast ausreizt (Schwerpunkt bei 1, 1.1 wäre der schon fast instabile Grenzfall),
erscheint die Strategie, nur die Position des 3. Steins zu ändern, nicht ganz sinnvoll. Wir können auf jeden Fall den 3. Stein um 1 gegenüber dem 2. Stein verschieben, dann bleibt das Gesamtsystem aus 2. und 3. Stein stabil. Wenn wir jetzt dieses System etwas weniger weit verschieben, können wir einen stabilen Turm bauen.
Wenn der 3. Stein um 1 gegenüber dem 2. und der 2. Stein um $\frac{1}{2}$ gegenüber dem 1. Stein verschoben ist, dann haben der 2. und der 3. Stein gemeinsam einen Schwerpunkt von $\frac{\frac{1}{2}+(1+\frac{1}{2})}{2}=1$ und wir erhalten wieder einen stabilen Turm.
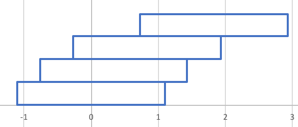
Wir können diesen 3er-Turm jetzt auf einen weiteren Stein stellen. Wie weit können wir denn diesen Turm gegen den Stein darunter verschieben und immer noch einen stabilen Turm erhalten?
Der Schwerpunkt des Turms aus 3 Steinen liegt bei
$\frac{0+\frac{1}{2}+(\frac{1}{2}+1)}{3}=\frac{2}{3}$, wir können den 3er-Turm also um $\frac{1}{3}$ gegenüber dem Stein darunter verschieben und erhalten immer noch einen stabilen 4er-Turm.
Probieren wir weiter: Der 4er-Turm hat den Schwerpunkt bei
$\frac{0+\frac{1}{3} + (\frac{1}{3}+\frac{1}{2})+(\frac{1}{3}+\frac{1}{2}+1)}{4}=\frac{3}{4}$,
wir können also diesen 4er-Turm auf einen weiteren Stein setzen und um $\frac{1}{4}$ verschieben und erhalten einen stabilen Turm der Höhe 5.
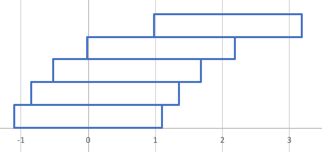
Das Prinzip funktioniert auch weiterhin. Bei einem Turm der Höhe $n$ nach dieser Bauart liegt der Schwerpunkt bei
$\frac{1}{n}$ und wir können ihn daher auf einen weiteren Stein draufsetzen und einen stabilen Turm der Höhe $n+1$ bauen.
Der Überhang dieses Turmes ist dann $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n-1}$.
Ein nach diesem Prinzip gebauter Turm der Höhe 10 sieht so aus:
Die Summe wird beliebig groß (Mathematiker sagen „die Summe divergiert“). Das kann man so sehen:
$$1+\frac{1}{2}+\underbrace{\frac{1}{3}+\frac{1}{4}}_{\geq 2\cdot\frac{1}{4}=\frac{1}{2}}+\underbrace{\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}}_{\geq 4\cdot\frac{1}{8}=\frac{1}{2}} +
\underbrace{\frac{1}{9} + … + \frac{1}{16}}_{\geq 8\cdot\frac{1}{16}=\frac{1}{2}}…+…$$
Daher können wir jeden beliebigen Überhang erreichen. Allerdings brauchen wir dazu ziemlich viele Steine. Für einen Überhang von 10 brauchen wird 12367 Steine.
Mathematisches Postskriptum (nur für Nerds):
Dass alle Schwerpunkte die gewünschte Eigenschaften haben, zeigt man mit vollständiger Induktion.
Wenn $S(n)$ der Schwerpunkt eines Turmes der Höhe $n$ ist, dann gilt
$S(n+1)=\frac{n}{n+1}(\frac{1}{n}+S(n))$. Mit $S(2)=\frac{1}{2}$ gilt dann $S(n)=\frac{n-1}{n}$.
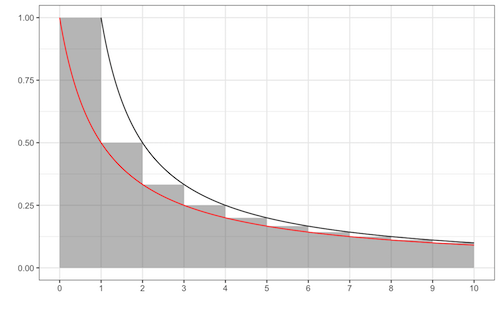
Mit Hilfe des grafischen Vergleichs der stetigen Funktionen $f(x)=\frac{1}{x}$ (schwarze Kurve) und $g(x)=\frac{1}{x+1}$ (rote Kurve) und der Sprungfunktion $h(x)=1/\lceil x \rceil$ (graue Blöcke)
und der Tatsache, dass der Logarithmus das unbestimmte Integral der Funktion $1/x$ ist, können wir eine Ungleichung über die Größe von $S(n)$ angeben.
$$\log(n+1) \leq S(n) \leq \log(n)+1$$
Durch Ungleichungsumformungen können wir daraus ableiten, dass für die Zahl $n$ der Steine, die notwendig sind, den Überhang $S$ zu erzielen, gilt:
$$e^{S-1} \leq n \leq e^S-1$$
Das Josephus-Problem
Eine genaue Beschreibung des Hintergrunds des Problems findet sich in der Wikipedia.
Problemstellung:
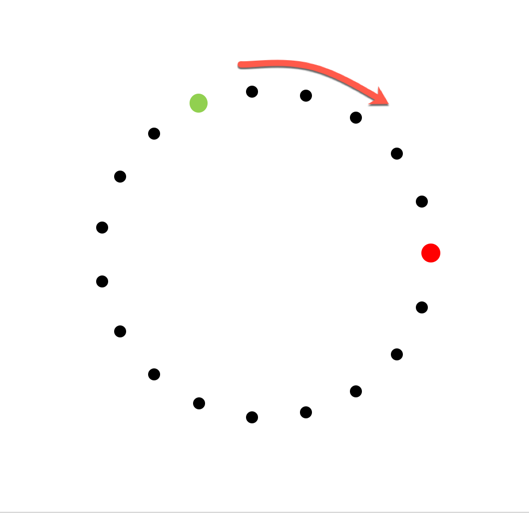
Eine bestimmte Zahl von Personen (n) steht im Kreis.
Es gibt eine „Startperson“. Geben wir ihr Nummer 1 und nummerieren wir fortlaufend im Kreis herum. Dann wird jede zweite Person aus dem Spiel genommen und zwar so lange, bis nur mehr eine Person übrig ist.
Bei 4 Personen werden also zunächst die Personen 2 und 4 aus dem Spiel genommen und wir sind wieder bei Person 1. Von dieser Startposition aus wird Person 3 aus dem Spiel genommen und 1 bleibt über.
Das gilt allgemeiner: Wann immer die Zahl der Personen gerade ist, dann ist man nach einer Runde genau wieder bei der ursprünglichen Startposition und das Verfahren wird fortgesetzt. Wenn die Zahl n eine Zweierpotenz ist (2, 4, 8, 16, …)ist, dann ist man nach jeder Runde an der Startposition und daher ist die Person an der Startposition auch die Person, die über bleibt.
Bei den anderen Zahlen ist die Überlegung etwas komplizierter. Sehen wir uns den Fall n=19 an.
Wenn man das Spiel komplett zu Ende durchspielt, dann sieht man, dass von Startperson 1 aus gezählt Person 7 über bleibt.
Wir können auch sagen: Bei 19 Personen ist die Person 6 Positionen vor der Startperson die, die über bleibt. (Vor bedeutet in Pfeilrichtung.)
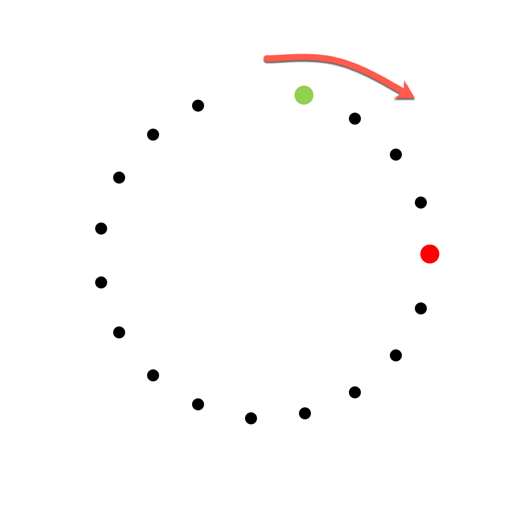
Wenn wir jetzt einen einzelnen Schritt des Ausscheidungsverfahrens durchführen, dann sehen wir folgendes Bild:
Wir haben eine neue Konfiguration mit n=18 und einer neuen Startposition. Die vorher und nachher rot markierte Position ist in beiden Fällen die Position der Person, die über bleibt.
Diese „Überbleibposition“ ist in der neuen Konfiguration 4 Schritte, also 2 Schritte weniger als in der alten Konfiguration von der Startposition entfernt. Das gilt fast immer, es gibt nur 2 mögliche Ausnahmen. Wenn die Startposition und die Überbleibposition identisch sind, dann funktioniert diese Überlegung nicht. Wenn die Überbleibposition nur einen Schritt hinter der Startposition läge, dann würde das ebenfalls nicht funktionieren. Die Position unmittelbar hinter der Startposition kann aber nie die Endposition sein, da die Person dort ja auf jeden Fall im nächsten Schritt entfernt wird.
Wir können diese Überlegung auch in umgekehrter Richtung anwenden. Wenn eine Position dazukommt, dann erhöht sich der Abstand zur Überbleibposition um 2.
Wir wissen also: Wenn n eine Zweierpotenz ist, dann ist die Startpostion auch die Überbleibposition.
Damit können wir die Überbleibposition für alle Fälle bestimmen. Für Zweierpotenzen ist 1 die Lösungszahl, und für jede
zusätzliche Position wird die Lösungszahl um 2 erhöht (wir müssen ja um 2 Positionen weitergehen). Sobad wir beim Dazugeben von Positionen zur nächsten Zweierpotenz kommen starten wir wieder mit Lösungszahl 1.
| Positionen | bleibt über |
| 1 | 1 |
| 2 | 1 |
| 3 | 3 |
| 4 | 1 |
| 5 | 3 |
| 6 | 5 |
| 7 | 7 |
| 8 | 1 |
| 9 | 3 |
| 10 | 5 |
| 11 | 7 |
| 12 | 9 |
| 13 | 11 |
| 14 | 13 |
| 15 | 15 |
| 16 | 1 |
| 17 | 3 |
| 18 | 5 |
| 19 | 7 |
| 20 | 9 |
Didaktische Nachbemerkung
Es gibt mehrere Möglichkeiten, die Lösung mathematisch abzuleiten und zu begründen. Die bekannteste davon findet sich im Buch „Concrete Mathematics“ von Donald Knuth, Ron Graham und Oren Patashnik. Eine andere Erklärung der Lösung mit einer sehr netten Animation gibt es bei Numberphile auf YouTube.
Bei beiden Erklärungen gibt es keine unmittelbar einleuchtende Begründung dafür, warum in den meisten Fällen eine zusätzliche Person die Lösungszahl um zwei erhöht. Hauptgrund ist, dass man in beiden Ansätzen über die Nummerierung der Personen, also einen absoluten Bezug spricht. Im obigen Ansatz spielt der Abstand zwischen Startposition und Endposition die wichtigste Rolle, und das ist ein relativer, kein absoluter Bezug. Mein Eindruck ist, dass dieser Wechsel des Beschreibungssystems den Lösungsweg leichter verständlich macht.