Methodisches zur Wählerstromanalyse
Methodische Bemerkungen
Wählerstromanalysen berechnet Schätzwerte für den Umfang der Wählerbewegungen zwischen den einzelnen Parteien. Sie verwendet dazu die Wahlergebnisse aller österreichischen Gemeinden sowie der Wiener Bezirke. Wahlkartenstimmen und Briefwahlstimmen können keinen Gemeinden zugeordnet und daher in der Analyse nicht verwendet werden. Diese Wähler und die Wähler von Kleinparteien erscheinen in der Gruppe der Nichtwähler.
Zunächst eine methodische Erläuterung am Beispiel des Vergleichs von NRW 2008 und der NRW 2013:
Grundlage der verwendeten Methode ist die Annahme, dass sich die Wähler einer bestimmten Partei von 2008 bei der späteren Wahl (also 2013) in allen Gemeinden der als homogen angenommenen Bundesländer nach etwa demselben Verteilungsschlüssel auf die 2013 kandidierenden Parteien aufgeteilt haben, dass also beispielsweise der Anteil aller SPÖ-Wähler von 2008, die 2013 die ÖVP gewählt haben, in allen Sprengeln eines solchen Gebiets annähernd gleich war. Ohne eine solche oder ähnliche Annahmen sind Wählerstromanalysen nicht möglich. Unter dieser Annahme lassen sich mit ziemlich aufwändigen mathematisch-statistischen Verfahren die Wählerströme schätzen, und man kann zusätzlich auch Schwankungsbreiten für diese Schätzwerte angeben. Für die politische Interpretation der Ergebnisse ist die Angabe von Schwankungsbreiten von hoher Bedeutung, weil Wählerbewegungen, deren Umfang mit hoher statistischer Absicherung angegeben werden kann, andere Schlussfolgerungen zulassen als mit hohen Unsicherheiten behaftete Schätzungen.
Da aus Wien nur die 23 Bezirksergebnisse und keine Ergebnisse in feinerer regionaler Gliederung zur Verfügung stehen sind die Schwankungsbreiten der Wiener Analyse relativ groß. Bei der Interpretation der Wiener Ergebnisse ist also Vorsicht geboten.
Verfahrensfragen
Bei Wählerstromanalysen gibt es drei Hauptprobleme technischer Natur:
Man muss eine eigene zusätzliche „Partei der Nichtwähler“ einführen, weil das Nichtwählen eine mögliche zu berücksichtigende Wählerentscheidung ist. Daher muss man auch Wählerströme von und zu dieser Gruppe berechnen und diese natürlich auch in der Analyse ausweisen. Selbstverständlich kann eine Wählerstromanalyse nur Auskunft über die Neuaufteilung der Wähler jener Parteien geben, die bei der betrachteten Vorwahl tatsächlich kandidiert haben.
Eigentlich geht das mathematische Modell der Wählerstromanalyse von der Fiktion der gleichen Wählerschaft bei beiden untersuchten Wahlen aus. Das entspricht natürlich nicht ganz der Wirklichkeit. Prinzipiell wäre es auch möglich, diese Änderung der Wählerschaft im Modell der Analyse zu berücksichtigen, allerdings stehen die dafür notwendigen Daten nicht zur Verfügung. Daher müssen wir uns mit einer Fiktion behelfen. Wir gehen von einer fiktiven Vorwahl aus, die etwa am Tage vor der aktuellen Wahl stattgefunden haben könnte, und bei der schon alle Wähler der neuen Wahl teilgenommen haben. Das (fiktive) Ergebnis dieser Wahl setzen wir so an, dass die Parteien dabei dieselben Anteile erreichen wie bei der realen Vorwahl. Das bedeutet ungefähr, dass wir zunächst einmal annehmen, dass die weggestorbenen Wähler und die Erstwähler bezogen auf die kandidierenden Parteien der Vorwahl etwa dieselbe Zusammensetzung aufweisen wie jene Wähler, die tatsächlich bei beiden Wahlen teilgenommen haben. Die berechneten Wählerströme beziehen sich dann auf den Vergleich der fiktiven Vorwahl mit der aktuellen Wahl. Hätten die weggestorbenen Wähler in höherem Maße für Partei A gestimmt als die restlichen Wähler und die hinzugekommenen Erstwähler in höherem Maß für Partei B, dann würde sich das in der statistischen Analyse als Wählerstrom von Partei A zu Partei B äußern.
Auch die Behandlung der Wahlkartenwähler passt nicht ganz mit dem Modell der Wählerstromanalyse zusammen.
Grundlage der Wählerstromanalyse sind die Wahlergebnisse der einzelnen Gemeinden. Wahlkartenwähler, die ihre Stimme in einem „fremden“ Wahlkreis abgeben, sind in diesen Gemeindeergebnissen aber nicht enthalten. Daher werden solche Stimmen in der Wählerstromanalyse den Nichtwählern zugerechnet. Stimmen von Wahlkartenwählern, die im eigenen Wahlkreis gewählt haben, werden in der Wählerstromanalyse möglicherweise einer falschen Gemeinde zugeordnet.
Statistische Methoden liefern bei sehr kleinen Parteien keine zuverlässigen und aussagekräftigen Schätzungen mehr. Daher werden in der vorliegenden Analyse nicht alle kandidierenden Parteien untersucht, sondern nur Parteien ab einer bestimmten Größe. Die restlichen Stimmen werden mit den Nicht- und Ungültig-Wählern zusammengefasst. Jene Gruppe, die wir in unserer Analyse mit der Abkürzung nw bezeichnen, besteht also aus den Nichtwählern, den Ungültig- Wählern und den Wählern der in der Analyse nicht gesondert ausgewiesenen Kleinstparteien.
Wählerstromanalyse Nationalratswahl 2013
- Die SPÖ hat vor allem an die Nichtwähler, aber auch an die FPÖ und FRANK verloren. Gewonnen hat die SPÖ Stimmen von BZÖ und in geringem Umfang auch von der ÖVP.
- Die ÖVP verlor vor allem an die NEOS und auch an die FPÖ.
- Die FPÖ gewann ein Drittel der früheren BZÖ-Stimmen und im wesentlich kleinerem Umfang auch Stimmen von ÖVP. Verloren hat die FPÖ an FRANK und an die Nichtwähler.
- Das BZÖ hat vor allem an die FPÖ verloren, aber auch an FRANK.
- Die GRÜNEn haben am stärksten an die NEOS verloren und Stimmen von BZÖ und früheren Nichtwählern gewonnen.
- FRANK hat die höchsten Gewinne vom BZÖ und die zweithöchsten Gewinne von der FPÖ.
- Die NEOS erzielten ihre höchsten Gewinne vom LIF, und etwas geringere Gewinne von den GRÜNEn und der ÖVP.
- Neu dazu gekommene Nichtwähler kommen vor allem von der SPÖ. Nur ganz wenige Nichtwähler von 2008 gaben 2013 eine Stimme für eine Partei ab.
Wählerströme in Stimmen (in Tausend)
Die Zahl 26 in der Zeile für das BZÖ und der Spalte für die SPÖ bedeutet, dass ca. 26000 Wähler vom BZÖ zur SPÖ gewechselt sind. Die statistische Schwankungsbreite dieser Schätzung findet man in der letzten Spalte der BZÖ-Zeile, sie beträgt ±18000
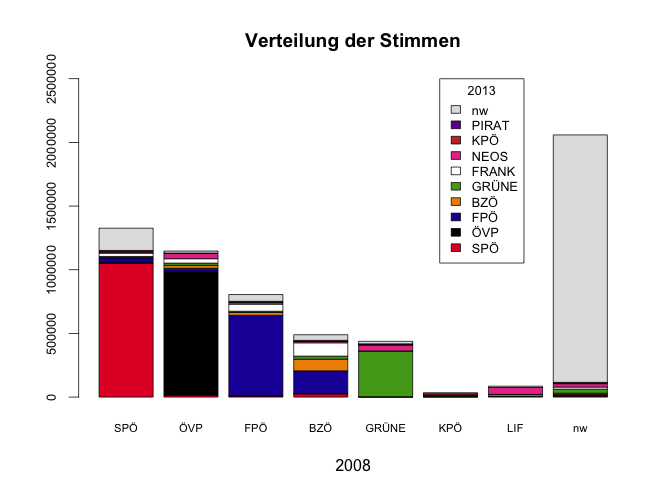
Verteilung der Stimmen
Die Zahl 5.4% in der Zeile für das BZÖ und der Spalte für die SPÖ bedeutet, dass 5.4% Wähler, die 2008 das BZÖ gewählt haben, zur SPÖ gewechselt sind. Die statistische Schwankungsbreite dieser Schätzung findet man in der letzten Spalte der BZÖ-Zeile, sie beträgt ±3.7%.
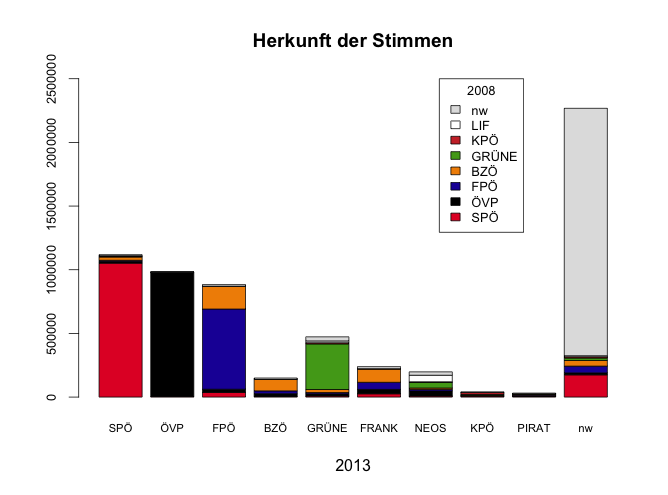
Herkunft der Stimmen
Die Zahl 2.4% in der Zeile für das BZÖ und der Spalte für die SPÖ bedeutet, dass 2.4% Wähler, die 2013 die SPÖ gewählt haben, vom BZÖ zur SPÖ gewechselt sind. Die statistische Schwankungsbreite dieser ist etwas komplizierter zu errechnen, eine Abschätzung der Genauigkeit lässt sich aber über die Tabelle mit den absoluten Stimmenzahlen ermitteln.
Grafische Darstellung
Der erste Balken der Grafik (mit SPÖ beschriftet) zeigt, wie die Wähler, die 2008 SPÖ gewählt haben, sich 2013 auf die kandidierenden Parteien aufgeteilt haben.
Der erste Balken der Grafik (mit SPÖ beschriftet) zeigt, welche Partei die Wähler, die 2013 SPÖ gewählt haben, 2008 gewählt haben.
Nachbemerkungen
Die statistische Methodik für Wählerstromanalysen wird in einem anderen Blogeintrag erklärt.
Welche statistischen Grafiken für Wählstromanalysen geeignet sind und warum ich immer noch die altmodischen Balkendiagramme verwende habe ich ebenfalls in einem Blogbeitrag kommentiert.
Wahlanalysen und Statistik – ein chronisches Leiden
Ich habe vor der Wahl in standard über die Leiden von Statistikern in Wahlzeiten geschrieben. Insbesondere über das, was man aus Umfragen erschließen kann und was nicht.
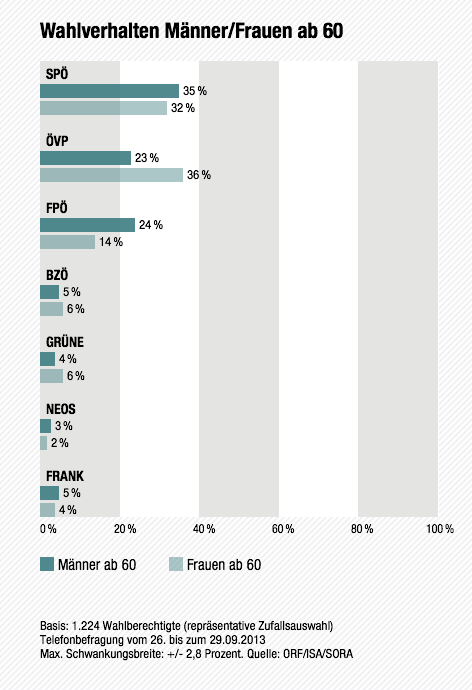
Und dann finde ich auf der ORF-Website folgende Grafik:
Das schmerzverursachende Detail ist die letzte Zeile. Etwa 1200 Befragte hats gegeben. Daraus ergibt sich eine Schwankungsbreite von +-2.8%.
Allerdings werden in der Grafik zwei Untergruppen der Befragten verglichen, nämlich Männer über 60 und Frauen über 60. Die Größe dieser Untergruppen wird nicht angegeben. Die braucht man aber zur korrekten Ermittlung der Schwankungsbreite.
Nehmen wir vereinfachend an, dass 1/3 der Wahlberechtigten über 60 ist. Und nehmen wir auch an, dass es etwa gleich viele Frauen und Männer gibt. Das stimmt nicht ganz, in der Altersgruppe gibts schon mehr Frauen. Aber wir wollen ja nur eine Überschlagsrechnung machen.
Also vergleichen wir 2 Gruppen der Größe je 200. Die Schwankungsbreite beträgt bei der Gruppengröße etwa +-6.4%.
Die 2.8%, die unter der Grafik ausgewiesen werden, gaukeln dem Leser eine Genauigkeit vor, die einfach nicht gegeben ist.
Und der Sicherheitsabstand, bei dem man bei 30%-Parteien statistisch einigermaßen gesichert von einem Unterschied zwischen den beiden untersuchten Gruppen ausgehen kann, beträgt 9.2%. Der Geschlechterunterschied zwischen Männern und Frauen ist also bei ÖVP und FPÖ statistisch gesichert, wenn der Anteil der auswertbaren Antworten hoch genug ist. Hätte der beispielsweise nur weniger als 70% betragen, dann wäre der Geschlechterunterschied für die FPÖ schon nicht mehr eindeutig statistisch gesichert.
Es ist ja schon ein Fortschritt, wenn jetzt (im Gegensatz zu früher) bei Umfragen Schwankungsbreiten angegeben werden.
Aber als Statistiker hab ich noch weitere (unbescheidene?) Wünsche: ich wünsch mir, dass da auch die richtigen Werte angegeben werden!
Umfragen, Wahlen und Statistik
Ich hab zum Thema „was kann man aus Umfragen erschließen“ im standard einen Kommentar der anderen geschrieben.
Und dann gibt’s natürlich noch den interaktiven Artikel in meinem Blog, mit dem man Schwankunsgbreiten auch selber ausrechnen kann.
Schultyp und Geschlecht bei PISA-Stichproben
Als im Dezember 2004 die Ergebnisse von PISA 2003 für Österreich publiziert wurden war allgemein von einem Absturz die Rede. Die Ergebnisse von 2003 waren deutlich schlechter als die Ergebnisse von 2000.
Schon damals bestand der Verdacht, dass für PISA 2000 durch die Gewichtung der einzelnen Schultypen und der Burschen und der Mädchen innerhalb der Schultypen in der Stichprobe die Aufteilung der Schüler im gesamten Altersjahrgang nicht richtig wiedergegeben wurde. Insbesondere gab es Hinweise darauf, dass die Berufsschüler (das sind die Schüler mit den schlechtesten PISA-Leistungen) deutlich unterrepräsentiert waren und deshalb die österreichischen PISA-Werte 2000 besser waren als sie es bei korrekter Gewichtung der Schultypen gewesen wären.
Die Gewichte für die Schultypen und Geschlechter waren zwar zunächst in den öffentlich verfügbaren Daten für PISA 2000 enthalten, wurden aber vor der Publikation der Daten für PISA 2003 auf Veranlassung der österreichischen PISA-Verantwortlichen mit Berufung auf Datenschutz aus den Daten entfernt. Die entsprechenden Daten für PISA 2003 wurden jedoch (wenn auch in etwas anderer Darstellung) veröffentlicht. Für PISA 2003 war der Datenschutz anscheinend kein so großes Anliegen.
Als Konsequenz war es jedenfalls nicht möglich, die Zusammensetzung der PISA-Stichprobe für 2000 und für 2003 zu vergleichen.
In einem Interview für profil vom 4.12.2004 (siehe profil Website) äussert sich der österreichische PISA-Verantwortliche so:
Dass der Absturz im Vergleich zu PISA 2000 wie in der Vorwoche kolportiert vor allem auf eine damalige falsche Gewichtung der Berufsschüler zurückzuführen ist, trifft nicht zu. Österreichs Schüler sind in den vergangenen Jahren schlicht schlechter geworden. Haiders Resümee: „Die Analysen zeigen, dass hinter den Differenzen eindeutig feststellbare Leistungsverluste der Schüler/innen stehen.“
Das Problem, dass die Gewichtung die Ergebnisse von 2000 verfälscht haben könnte, wurde also in Abrede gestellt.
Die Diskussionen darüber, ob jetzt die PISA-Ergebnisse von 2003 wirklich um vieles schlechter als die Ergebnisse von 2000 waren, führten schlussendlich dazu, dass das Bildungsministerium eine Studie in Auftrag gab, die die Qualität der Stichproben näher untersuchen sollte.
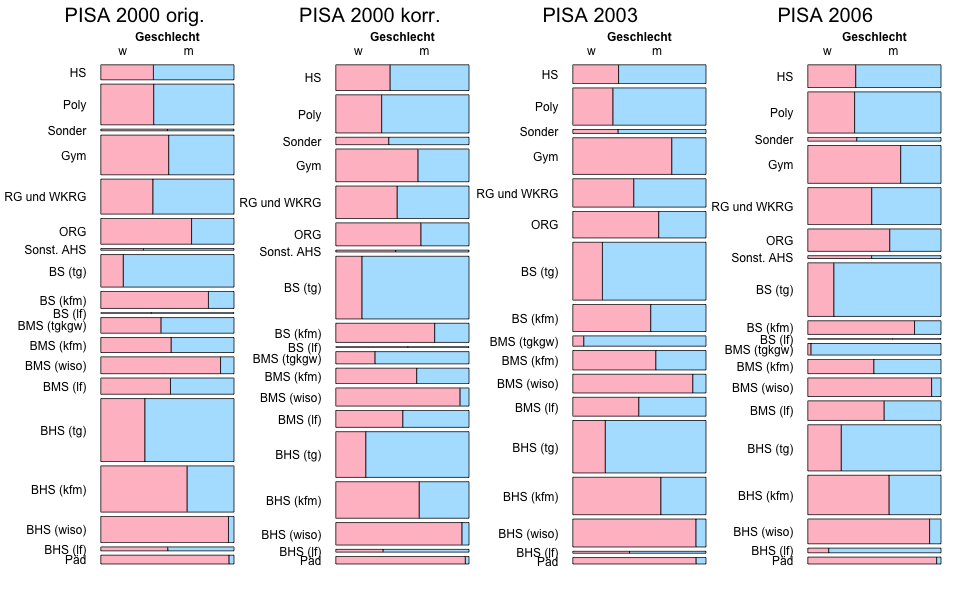
Im Zuge dieser Untersuchung stellte sich heraus, dass die Gewichtung der Schultypen und Geschlechter in der PISA-Stichprobe tatsächlich ganz wesentlich von den entsprechenden Anteilen an der Schülerpopulation abwich. Eine Forschergruppe von Statistikern erarbeitete ein neues korrigiertes Gewichtungsschema, das die Anteile der Schülergruppen korrekt wiedergibt. Die folgende animierte Grafik ermöglicht einen Vergleich des ursprünglichen und des korrigierten Gewichtungsschemas.
Stichprobe PISA 2000 Österreich
Diese Grafik soll durch das „Springen“ der Balkenbreiten die sehr grossen Unterschiede zwischen den unkorrigierten und den korrigierten Gewichten darstellen. Sie können die Animation mit den Steuerungselementen darunter stoppen, und sie können mit den „Pfeilknöpfen“ zwischen den Bildern wechseln. Wenige Absätze weiter unten finden sie die Grafiken noch einmal ohne Animation. Dort kann man die Anteile der Schultypen und Geschlechter „in Ruhe“ vergleichen.
Die Grafik zeigt, dass zunächst Berufsschulen (BS) deutlich zu gering und Berufsbildende Höhere Schulen (BHS) deutlich zu hoch gewichtet wurden. Da BHS gute und BS schlechte PISA-Leistungen erbringen hatte das zur Folge, dass die PISA-Werte für 2000 nicht den tatsächlichen Verhältnissen entsprachen sondern ein zu schön gefärbtes Bild zeichneten. Am deutlichsten sind die Gewichtungsunterschiede übrigens bei BS (tg) zu sehen.
Für 2006 und 2009 sind die Daten über die Gewichtung der Schultypen und Geschlechter (so wie für 2000) wieder nicht verfügbar. Dem Autor dieses Blogs standen sie allerdings im Rahmen von vom Bildungsministerium in Auftrag gegebenen Untersuchungen zur Verfügung. Die folgende Grafik zeigt die Gewichtungsschemata daher für 2000 (unkorrigiert und korrigiert), 2003 und 2006. Die Daten für 2009 sind weder in den öffentlich verfügbaren Daten enthalten noch standen sie dem Autor dieses Blogs zur Verfügung. Daher kann man die Gewichte der Schultypen und Geschlechter für PISA 2009 nicht überprüfen und darstellen.
Diese Grafik zeigt merkbare Schwankungen bei der Aufteilung der Schüler auf die verschiedenen Typen von BHS und BS. Auch der Mädchenanteil in den Gymnasien ist in den verschieden Jahren deutlich verschieden.
Die Auffälligkeiten bei der Gewichtung führten jedenfalls (wie schon gesagt) dazu, dass die vom Bildungsministerium beauftragte Gruppe unabhängiger Statistiker (A.Prof. Dr. Erich Neuwirth, Univ.Prof. Dr. Wilfried Grossmann, Univ.Doz. Dr. Ivo Ponocny) die Stichprobenproblematik näher untersuchte. Diese Gruppe hat das in den Grafiken als „PISA 2000 korr.“ ausgewiesene Gewichtungsschema erarbeitet. Diese Gewichtung wurde von der OECD offiziell als notwendige Korrektur anerkannt und alle neueren PISA-Publikationen verwenden die nach diesem korrigierten Schema berechneten Kennwerte für Österreich. Untersuchungen durch ein unabhängiges Wissenschafterteam können also bewirken, dass von den PISA-Verantwortlichen zunächst verbreitete Irrmeinungen über die Leistungsfähigkeit österreichischer Schüler korrigiert werden können und diese Korrekturen auch von den internationalen PISA-Verantwortlichen als notwendig und richtig anerkannt werden.
Einer der ersten Hinweise darauf, dass das ursprüngliche Gewichtungsschema für PISA 2000 fehlerhaft war, war übrigens, dass es laut Stichprobe mehr Schülerinnen als Schüler gegeben hätte. Es ist aber eine allgemeine bekannte demografische Tatsache, dass in jedem Geburtenjahrgang etwas mehr Buben als Mädchen geboren werden. Bei PISA 2003 und PISA 2006 stimmte das Geschlechterverhältnis in der Stichprobe mit dieser Tatsache überein. Bei PISA 2009 gäbe es laut Stichprobe (so wie 2000 vor der Korrektur) ebenfalls wieder mehr Mädchen als Burschen, die noch in schulischer Ausbildung stehen. Das ist ein deutlicher Hinweis darauf, dass man die Gewichtung der Stichprobe auch für 2009 einer Untersuchung durch unabhängige Experten unterziehen sollte.
Die Abkürzungen für die einzelnen Schultypen bedeuten übrigens folgendes:
HS = Hauptschule
Poly = Polytechnische Schule
Sonder = Sonderschule
Gym = Gymnasium
RG und WKRG = Realgymnasium und wirtschaftskundliches RG
ORG = Oberstufenrealgymnasium
Sonst. AHS = Sonstige Allgemeinbildende Schulen/mit Statut
BS = Berufsschule
BMS = Berufsbildende Mittlere Schule
BHS = Berufsbildende Höhere Schule
Päd = Anstalten der Lehrerbildung und Erzieherbildung
tg = technisch-gewerblich
kfm = kaufmännisch
tgkgw = technisch-gewerblich-kunstgewerblich
wiso = wirtschaftsberuflich-sozialberuflich
lf = land- und forstwirtschaftlich