Zugang zu Bildungsforschungsdaten
Der standard hat mich zum Thema „Zugang zu Bildungsforschungsdaten“ interviewt. Sie können hier nachlesen was ich dazu meine.
PISA 2012 – wer wird besser, wer wird schlechter
Wenn die PISA-Ergebnisse veröffentlicht werden wird oft gefragt, wer sich verbessert und wer sich verschlechtert hat.
Man könnte sich natürlich einfach die Tabellen mit den Ergebnissen ansehen, aber es gibt informativere Darstellungsformen.
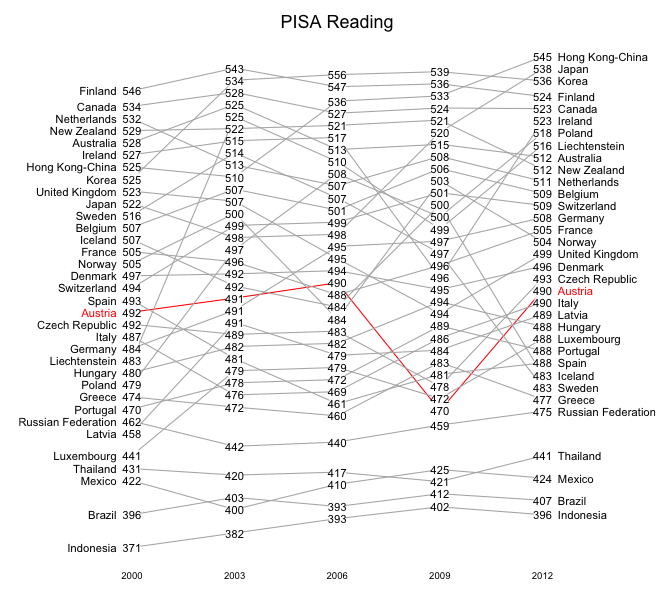
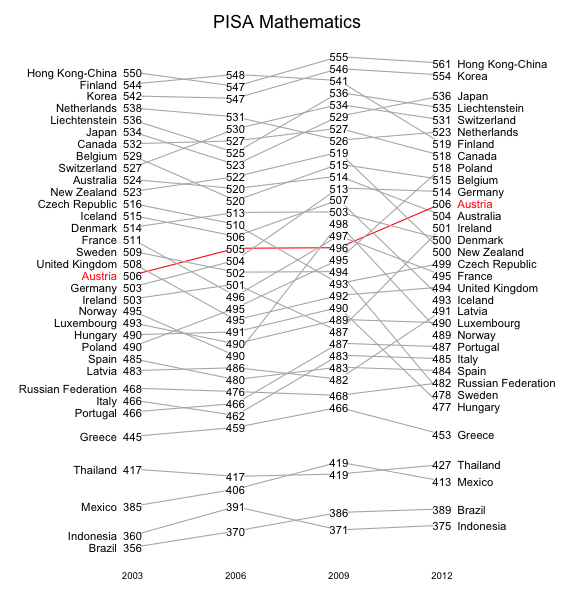
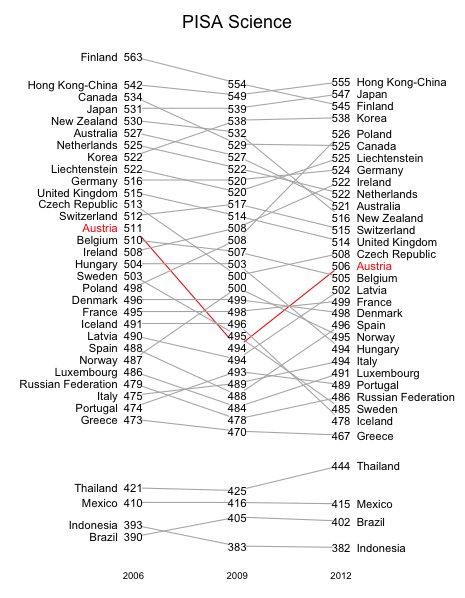
Die folgenden Grafiken zeigen annähernd den Verlauf der PISA-Punktewerte für alle jenen Länder, die an allen bisherigen PISA-Tests teilgenommen haben. Die Position der Datenpunkte entspricht nicht ganz genau den Werten, weil es da zu Überlagerungen kommen würde,
die das Ablesen in der Grafik erschweren würde. So kann es sein, dass eine Verbindungslinie zwischen 2 Punkten leicht nach oben geneigt ist, obwohl die Punktewerte geringfügig abgenommen haben. Starke Veränderungen nach oben oder nach unten werden aber in der Grafik annähernd richtig wiedergegeben.
Vereinfacht gesagt wird dir Grafik so erzeugt: Für das Land mit dem schlechtesten Werten (beim Lesen z.B. Indonesien) zeichnet man die Kurve richtig. Dann zeichnet man die weiteren Länder aufsteigend von den schlechteren zu den besseren so, dass man immer dann, wenn ein Punkte einen vorherigen Punkt überdecken würde, den neuen Punkt nach oben verschiebt.
Wie stark die Verzerrungen durch das Verschieben der Punkte sein können sieht man daran, dass die Verbindungslinie für die österreichischen Mathematikergebnisse 2006 und 2009 waagrecht ist, obwohl die Punktezahl sich um 9 verringert hat. Die entsprechende Verschlechterung um 18 Punkte beim Lesen wird aber grafisch deutlich erkennbar.
Die Verschiebungen hängen auch davon ab, wie sich die jeweils besten und schlechtesten Werte der anderen Länder verändert haben.
Auch die Position eines Landes innerhalb aller untersuchten Länder spielt eine Rolle. Wenn sich der Werte eines Landes kaum ändert aber mehrere andere Länder zunächst besser, später aber schlechter als das untersuchte Land sind, dann zeigen die Verbindungslinien dieses Landes nach oben. Das ist teilweise bei den österreichischen Mathematik-Ergebnissen der Fall.
Und jetzt die Grafiken:
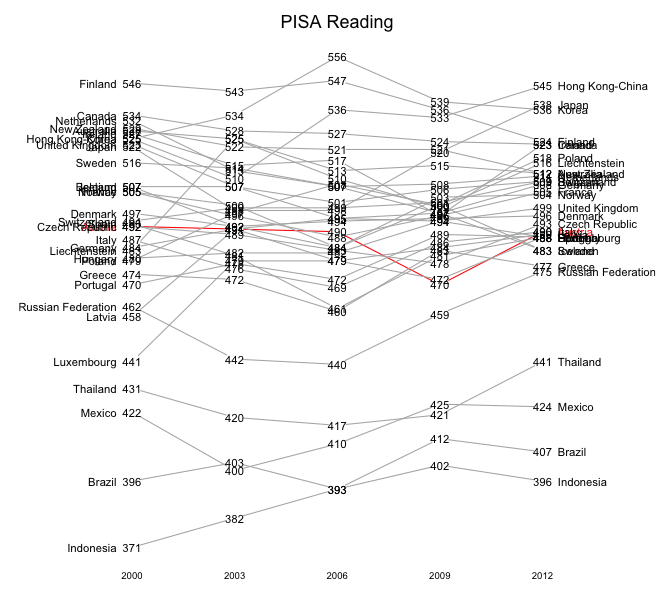
Und warum das Herumschieben der Punkte notwendig ist zeigt die folgende Grafik. Da sind die Werte der einzelnen Länder „maßstabsgetreu“ eingezeichnet.
Erste Anmerkungen zu den PISA-2012-Ergebnissen
Die OECD hat einen eigenen kleinen Bericht über die österreichischen PISA-Ergebnisse zum download veröffentlicht.
Dort sind nicht alle früheren Ergebnisse angeführt, deswegen weisen wir hier die Ergebnisse aller bisherigen PISA-Tests zur Übersicht aus.
| Lesen | Mathe | Naturw | |
|---|---|---|---|
| 2000 | 492 | 503 | 505 |
| 2003 | 491 | 506 | 491 |
| 2006 | 490 | 505 | 511 |
| 2009 | 470 | 496 | 494 |
| 2012 | 490 | 506 | 506 |
Einige Zahlen in dieser Tabelle sind fett gedruckt. Warum?
Die OECD ist der Meinung, dass man Längsschnittvergleiche erst ab jenem Zeitpunkt machen sollte, an dem eine der 3 Domänen erstmals Hauptdomäne war. Das war bei Lesen 2000, bei Mathematik 2003 und bei den Naturwissenschaften 2006. Das sind die fettgedrucken Zahlen.
Warum sind die Zahlen in der Zeile für das Jahr 2009 kursiv gedruckt? Die OECD schränkt (auch im oben verlinkten Bericht) die Interpretationsmöglicheiten der Ergebnisse für 2009 drastisch ein und meint, dass diese Zahlen für Längsschnittvergleiche nicht geeignet sind.
Zur Erinnerung: Damals gab es von manchen Schülervertretern einen Boykottaufruf und deswegen musste eine doch merkbare Anzahl von Testbögen als nicht auswertbar ausgeschieden werden. Das hat wahrscheinlich das Testergebnis für 2009 etwas verzerrt.
Lässt man 2009 einmal außer Acht, dann sind die Ergebnisse für Mathematik und Lesen für alle anderen Tests praktisch gleich.
Da kaum anzunehmen ist, dass es in einem doch recht trägen Bildungssystem innerhalb von 3 Jahren zu einem dramatischen Absturz und in den 3 folgenden Jahren zu einem Aufschwung zu alten Höhen kommt, sollte man die Abweichung der Ergebnisse von 2009 aufgrund einer deutlich anderen psychologischen Situation beim Tests mit höchster Vorsicht interpretieren.
Ein bisschen komplizierter ist die Lage bei den Naturwissenschaften. Wenn man aber weiß, dass die OECD vor allem nach den erkannten Instabilitäten der Messung bei den Naturwissenschaften meint, dass man Längsschnittvergleiche erst ab dem Zeitpunkt, wo eine Domäne Hauptdomäne war, anstellen sollte, dann sollte man die Naturwissenschaftsergebnisse erst ab 2006 heranziehen. Und dann gibts wieder die bekannten Probleme mit den Ergebnissen von 2009 und übrig bleibt, dass wir uns von 2006 auf 2012 geringfügig verschlechtert haben.
Die OECD kommentiert auch, dass sich der Unterschied zwischen Buben und Mädchen von 2003 auf 2012 sehr vergrößert hat.
Auch das ist mit Vorsicht zu interpretieren. Die Ergebnisse von PISA 2003 hatten kleinere methodische Fehler, und das Ergebnis der Mädchen war damals „zu gut“, weil in der Stichprobe mehr AHS-Schülerinnen als in der Gesamtpopulation waren und das durch die offizielle Gewichtung nicht ausgeglichen wurde. Nachzulesen ist das in unserem Buch und im Internet. In den korrigierten Werten (und wir bergünden unserer Korrekturen und liefern auch die entsprechenden Daten!) war der Geschlechterunterschied in Mathematik auch 2003 schon um 5 Punkte größer als in den offiziellen Publikationen ausgewiesen. Es gibt dann immer noch eine Zunahme des Unterschieds von 2003 auf 2012, aber doch weniger dramatisch als das in den OECD-Berichten dargestellt wird.
Im wesentlichen sind die österreichischen Ergebnisse im längerfristigen Vergleich also gleich geblieben.
Wenn wir uns in den Rankings im Vergleich zu 2009 verbessert haben dann ist das nicht besonders interessant, weil die Ergebnisse von 2009 vor allem im Lichte der vorliegenden Ergebnisse als nicht besonders aussagekräftig anzusehen sind.
Und wenn wie einen besseren Platz in Rankings feiern, obwohl unsere Werte gleich geblieben sind, dann heisst das, dass wir uns darüber freuen, dass unserer Schüler zwar nicht klüger, die in ein paar anderen Ländern aber leistungsschwächer geworden sind. Das wäre dann doch ein sehr seltsames Verständnis der Aufgaben unseres Bildungssystems!
Mathematik und Mathematikunterricht – getrennte Welten
Michael Hufnagl mach im Kurier seinem Ärger über den Mathematikunterricht sehr deutlich Luft.
Für mich als Mathematiker, der sein Fach sehr mag, ist das sehr schmerzhaft.
Er hat in dem, was er sagt, großteils recht, aber es gibt doch einiges anzumerken. Die Mathematik, die er meint, ist die Mathematik, die meist in der Schule vermittelt wird. Und die ist ziemlich weit entfernt von dem, was Mathematik im Alltagsleben vieler Leute bedeutet oder bedeuten kann.
Ich bilde (auch noch als Pensionist) an der Universität Wien angehende Informatik-Lehrer aus. Da ist Mathematik unvermeidbar und ich bin daher in die Problematik durchaus eingearbeitet. Mein Studierenden müssen sich immer wieder folgenden Vergleich anhören:
Wenn wir einen Vergleich zwischen Mathematik und Musik machen, dann beschäftigt sich der Mathematikunterricht in der Schule „mit typografischen Feinheiten der Notenschrift“, die Schüler „hören aber keine Musik“ und sie erhalten auch keine Gelegenheit, „Musikinstrumente zu erproben“.
Wenn wir das ändern wollen ist allerdings radikales Umdenken beim Formulieren der Ziele des Mathematikunterrichts notwendig.
Ich möchte an einem kleinen Beispiel illustrieren, wo die Problematik des Mathematikunterrichts derzeit liegt.
Ich bin (mea maxima culpa) auch Schulbuchautor. Zuständig u.a. für Statistik in einem Schulbuch für die 3. und 4. Klasse AHS. Ich wollte im Schulbuch ein Beispiel (mit echten, an meinen Studenten erhobenen) Daten darüber, ob Kinder eher zu Rauchern werden, wenn ihre Eltern rauchen.
Die Verlagslektorin wollte verhindern, dass dieses Beispiel ins Buch kommt. So ein Thema sei nicht schulbuchgeeignet.
Ich wollte es damit nicht bewenden lassen und habe recherchiert. Im Deutschbuch derselben Schulstufe gibts Vorschläge für Diskussionen, weil man im Deutschunterricht auch Argumentieren lernen soll. „Rauchverbot Ja oder Nein“ war dort einer der Themenvorschläge. Damit konfrontiert war die Verlagslektorin der Meinung, dass man das ja vielleicht im Deutschunterricht machen könne; im Mathematikunterricht habe etwas mit derartigem Bezug zum Alltagsleben und zur Gesellschaft aber nichts verloren.
Nach langen Diskussionen hab ich mich doch durchgesetzt, das Beispiel ist im Buch der 3. Klasse jetzt drinnen. Ich wollte es allerdings zum Aufhänger eines ganzen Abschnitts machen, weil ich zeigen wollte, dass Datenanalyse ein wichtiges Instrument zum Verständnis der Welt um uns sein kann. Das ist mir nicht gelungen. Es ist „nur“ ein Rechenbeispiel.
Dass es die Diskussion überhaupt gegeben hat zeigt für mich ganz deutlich, wo die Probleme des Mathematikunterrichts liegen.
Ich würde mir natürlich wünschen, dass der Deutschunterricht und der Mathematikunterricht so abgestimmt werden, dass bei Argumentieren im Deutschunterricht die Einsichten, die man aus der Datenanalyse im Mathematikunterricht hoffentlich gewinnt, einfließen.
P.S.: Auch die Taktung der Schule in 50-Minuten-Einheiten ist ein fundamentales Problem für den Mathematikunterricht. Viele spannende Probleme lassen sich meist nicht in derart kurzer Zeit „zu Ende denken“. Auch deswegen ist die Diskussion um die Lehrerdienstrechtsreform so absurd: Dort geht es darum, wie viele dieser 50-Minuten-Einheiten neue LehrerInnen unterrichten sollen. Dabei sollten neue LehrerInnen sich vor allem von der 50-Minuten-Taktung befreien können. Jetzt schon angestellte LehrerInnen übrigens auch.
Wählerstromanalysen und statistische Grafiken
Der ORF hat bis vor kurzem zur grafischen Darstellung von Wählerstromanalysen die „fliegenden Plättchen“ verwendet. Man hat ähnliche Darstellungen auch im Web gefunden. In gedruckten Zeitungen war das nicht möglich weil die Animation (also ein Bewegungsablauf) essentieller Teil dieses Grafiktyps ist.
Diesmal gab es eine neue Grafik, nennen wir sie „Stromdiagramme“. In der Fachterminologie heißen diese Diagramme nach einem der ersten Verwender Sankey-Diagramme (genaueres siehe Wikipedia)
Ein Beispiel dazu findet sich im standard.
Auch der ORF hat diese Grafikform verwendet.
In meinen Wählerstromanalysen verwende ich immer noch eine schon recht alte Form der statistischen Grafik, nämlich gestapelte Balkendiagramme.
Ich könnte auch die anderen Grafiktypen verwenden. Warum mache ich das nicht?
Dazu eine grundsätzliche Frage:
Wozu stellt man Wählerstöme überhaupt grafisch dar? Wohl vor allem, damit der Leser oder Zuschauer die Größen der Ströme gut vergleichen kann.
Die fliegenden Plättchen haben diesen Vergleich immer schon schwer gemacht. Die Größe eines Wählerstroms wird bei dieser Grafikdarstellung durch die Anzahl der nacheinander fliegenden Plättchen ausgedrückt. Man muß also mitzählen und kann nicht mit einem Blick sehen, dass ein Wählerstrom doppelt so groß wie ein anderer ist. Eigentlich wird bei dieser Form der Grafik der Verpackungseffekt (es schaut halt so nett aus) der wichtigsten Aufgabe einer statistischen Grafik – die Daten besser verständlich zu machen – geopfert.
Die Stromdiagramme sind in letzter Zeit sehr populär geworden, weil es einfach verwendbare Implementation für Webseiten gibt (z.B. in der Grafik-Bibliothek d3.js)
Als interaktive Grafik auf dem Web hat diese Darstellungsfrom auch wirklich ihre Stärken:
Die Breiten der „Stromlinien“ geben den Umfang des Wählerstroms an und wenn man die Maus über einen Strom bewegt sieht man die Beschreibung und die Wählerzahl. Der große Vorteil ist, dass man selber aussuchen kann, welches Detail man gerade genauer studieren möchte. Wenn man das Diagramm statisch vor sich sieht, dann ist es nicht besonders übersichtlich, das „Hineinzoomen“ in Details nach den eigenen Bedürfnissen macht diese Form aber sehr hilfreich.
Wenn man diese Grafik aber – so wie im ORF – mit fixem Ablauf vorgespielt bekommt, dann geht der wichtigste Aspekt, die Möglichkeit der selbstgesteuerten selektiven Hervorhebung verloren. Für statistische Darstellung im Fernsehen erscheint mir (und anderen Statistikern) diese Form daher ziemlich ungeeignet.
In einem gedruckten (statischen) Medium kann diese Form bei Wählerstromanalysen auch nicht das Wichtigste, die bessere Verständlichkeit der statistischen Daten, leisten.
Die ganz einfachen Balkendiagramme (wie etwa hier) sind ziemlich leicht verständlich und zeigen sehr klar den Umfang der einzelnen Wählerströme. Man erkennt bei den numerisch wichtigen Wählerströmen auf den ersten Blick, welcher Strom um wieviel größer als welcher andere war.
Bei statistischen Grafiken können modernere und interaktive Darstellungsformen nicht automatisch die Daten besser verständlich machen als ganz alte Darstellungsformen.
Übrigens ist die Grundidee der Sankey-Diagramme, die Breite von Verlaufslinien dazu zu verwenden, Mengenangaben zu illustrieren, schon sehr alt. Sie ist bei manchen Phänomenen auch für gedruckte Darstellung geeignet.
Ein sehr berühmtes Beispiel ist die Darstellung von Napoleons Russlandfeldzug von Charles Minard