Das Assoziativgesetz – was ist das und warum ist das wichtig?

Im Mathematikunterricht lernt man

$$(a+b)+c=a+(b+c)$$

Das ist das Assoziativgesetz.

Als Zeichenkette aus Buchstaben und mathematischen Zeichen ist das nicht besonders beeindruckend, und man sieht auch nicht, warum das wichtig ist.

Praktisch verwendet man es oft, ohne dass man es merkt.

Wenn man beispielsweise $25+27+23$ berechnen soll, dann kann man zuerst $25+27=52$ berechnen und dann $52+23=75$ berechnen, um das Ergebnis zu erhalten. Man kann aber auch „sehen“, dass $27+23=50$ ist, und braucht dann nur $25+50=75$ zu berechnen. Die zweite Art der Berechnung ist „handlicher“, und das Assoziativgesetz ist der Grund, dass wir sicher sein können, bei beiden Rechnungen dasselbe Ergebnis zu erhalten.

Man kann das Assoziativgesetz auch sehr anschaulich illustrieren.
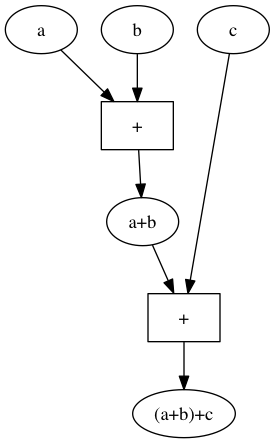
Wenn man $(a+b)+c$ als grafische Rechenmaschine darstellt sieht das so aus:

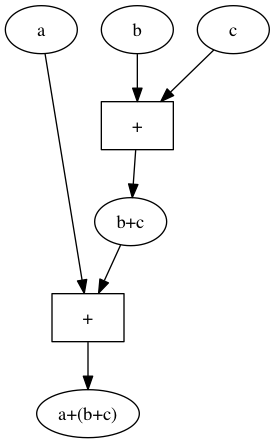
Die grafische Darstellung von $a+(b+c)$ sieht so aus:

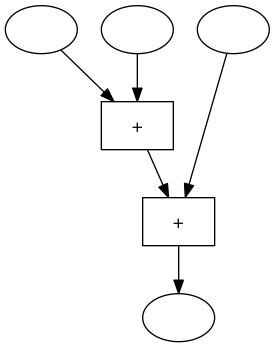
Wir können diese beiden „Rechenmaschinen“ auch ohne die Variablennamen veranschaulichen. Jede dieser Maschinen hat 3 Inputs und einen ouput. Im Inneren der Maschine gibt es 2 Addierwerke. Die erste Maschine addiert den ersten und den zweiten Input und addiert dann zu dieser Summe den dritten Input.

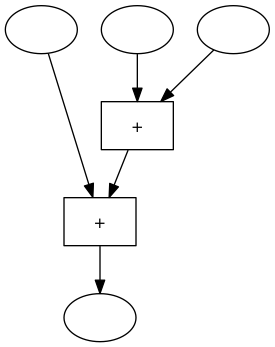
Die zweite Rechenmaschine addiert zuerst den zweiten und den dritten Input und addiert dann zu dieser Summe den ersten Input:

Die Rechenwerke in diesen Maschinen sind verschieden verdrahtet, aber wir wissen, dass beide Maschinen bei gleichen Inputs immer dasselbe Ergebnis liefern.

Wir können das dazu verwenden, andere Maschinen, in denen diese 3er-Addiermaschine als Teil vorkommt, umzubauen.

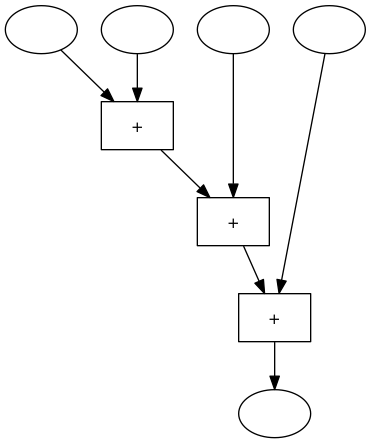
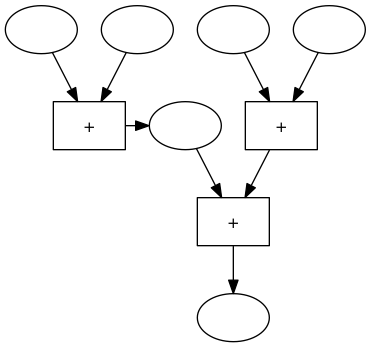
Eine einfache Maschine zum Addieren von 4 Zahlen sieht so aus:

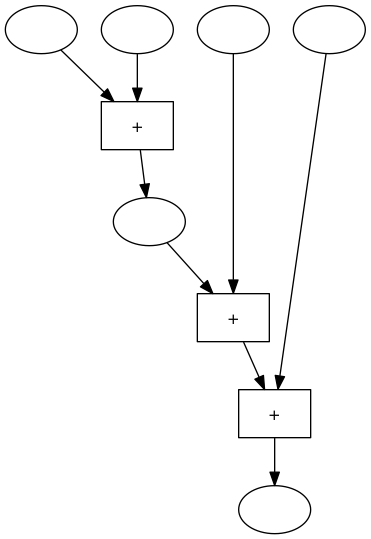
Wir markieren in dieser Maschine ein Zwischenergebnis mit einem Oval

und wir verschieben die Blöcke in der Maschine ein bisschen

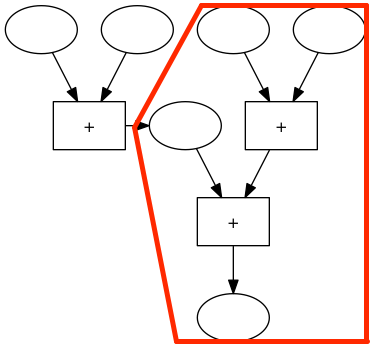
Im rechten Teil diese Maschine gibt es einer 3er-Addiermaschine:

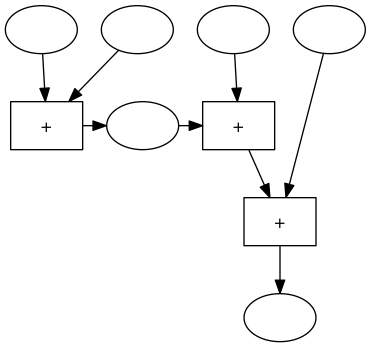
Diese Maschine können wir durch eine andere 3er-Addiermaschiene, die immer dasselbe Ergebnis liefert, ersetzen:

In dieser Maschine

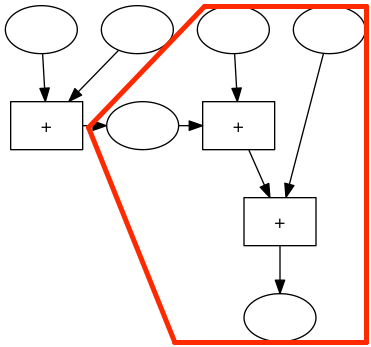
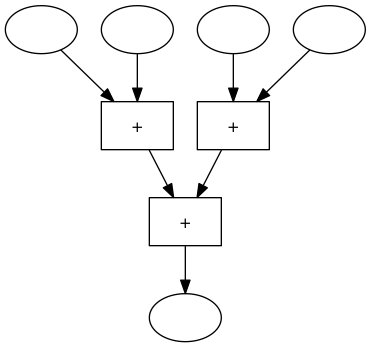
können wir den Block für das Zwischenergebnis wieder entfernen und die Blöcke noch etwas verschieben und erhalten dann folgende Maschine:

Und wozu das ganze?

In der usprünglichen 4er-Addiermaschine mussten 2 der 3 Rechenwerke auf das Ergebnis des vorgeschalteten Rechenwerks warten. In der neuen 4er-Addiermaschine können 2 Rechenoperationen gleichzeitig durchgeführt werden. Die erste Maschine braucht also 3 Zeiteinheiten für das Addieren von 4 Zahlen, die zweite Maschine braucht nur 2 Zeitschritte, sie kann also schneller rechnen.

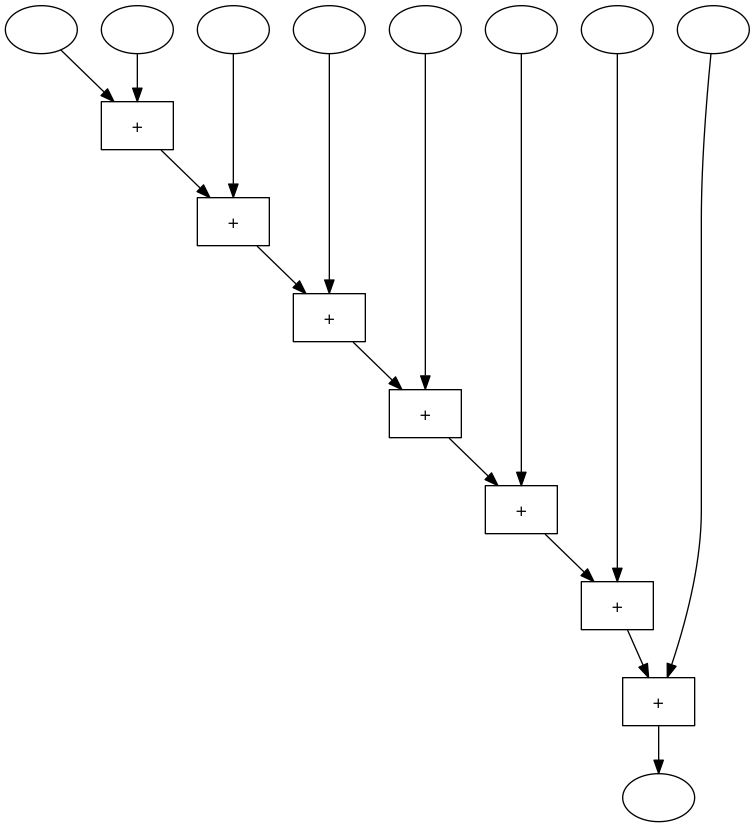
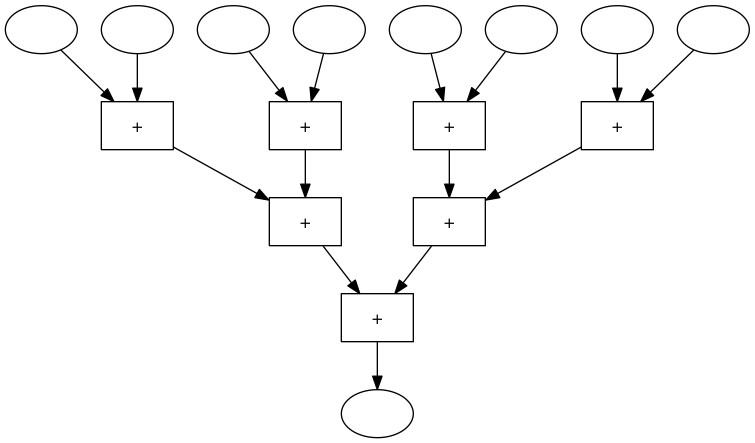
Eine 8er-Addiermaschine die immer eine Zahl zur vorherigen Summe addiert, sieht so aus:

Wenn man in dieser Maschine merhmals 3er-Maschinen durch funktionsgleiche 3er-Maschinen ersetzt, dann erhält man folgende Maschine:

Die ursprüngliche 8er-Maschine brauch 7 Zeitschritte, die umgebaute Maschine nur 3.

Das Umbauen der Maschine funktioniert nur, weil das Assoziativgesetz gilt.

Geschicktes Anwenden dieses Gesetzes führ also dazu, dass man bei bestimmten Aufgaben wesentlich schneller Rechnen kann.

Parallele Computerarchitektur ist eine der neuen Entwicklungen der Computertechnik. Was wir hier beschrieben haben ist eines der Prinzipien, nach denen parallele Programme arbeiten.

Wahlprognose, Wahlhochrechnung und Wahlanalyse –
was denkt sich ein Statistiker dazu

In der nzz.at habe ich einen Artikel mit dem Titel

Wahlumfragen taugen nicht für Prognosen

publiziert. Dieser Artikel ist eine leicht modifizierte Form des folgenden Textes:

Bei der Gemeinderatswahl in Wien war die 17-Uhr-Prognose des ORF ziemlich weit vom Endergebnis entfernt. Insbesondere gab es Fehlinformationen über Gleichstand oder Vorsprung zwischen SPÖ und FPÖ. Die erste Hochrechnung (um 18 Uhr) war dann schon sehr treffsicher; insbesondere prognostizierte sie schon den deutlichen Abstand zwischen SPÖ und FPÖ.
Wieso konnte die erste Prognose so schiefgehen?
Die Wahlprognose von 17 Uhr beruhte auf einer Umfrage, die Hochrechnung um ca. 18 Uhr dagegen auf tatsächlichen Wahlergebnissen aus Wahlsprengeln. Der Auszählungsgrad der ersten Hochrechnung betrug 13,9%. Wieso gab es um 17 Uhr noch kein zuverlässige Hochrechnung?
Bei den Wiener Wahlen schließen alle Wahllokale gleichzeitig um 17 Uhr. Bei anderen Wahlen (Landtagswahlen, Nationalratswahlen, Bundespräsidentenwahlen) gibt es viele Wahllokale, die schon früher schließen. Daher stehen bei den anderen Wahlen beim Wahlschluss (bei bundesweiten Wahlen um 17 Uhr, bei manchen anderen Wahlen früher) schon viele ausgezählte Ergebnisse zur Verfügung. In Wien gab es um 17 Uhr noch kein ausgezähltes Sprengelergebnis.
Daher wurde im ORF beschlossen, eine Prognose auf Grundlage einer sehr knapp vor der Wahl durchgeführten Umfrage durchzuführen. Laut Beschreibung der ORF-Hochrechner wurden dazu in den letzten Tagen vor der Wahl etwa 2200 Wahlberechtigte telefonisch befragt. Die prognostizierten Parteienanteile wurden allerdings nicht direkt dieser Umfrage entnommen, sondern mit Hilfe einer Rückerinnerungsfrage („welche Partei haben sie denn das letzte Mal gewählt“) nachjustiert. Die Forscher des SORA-Instituts sagen, dass es offensichtlich bei der Rückerinnerungsfrage zu Problemen gekommen und daher die Nachjustierung der Umfrageergebnisse schiefgegangen ist.
Wahlprognosen zum Wahlschluss ohne ein einziges ausgezähltes Teilergebnis gibt es auch in Deutschland. Dort darf nämlich erst mit der Auszählung begonnen werden, wenn alle Wahllokale bereits geschlossen haben. Die 18-Uhr-Prognosen in Deutschland (dort ist der Wahlschluss später) sind ziemlich treffsicher. Wie schafft man das in Deutschland?
Die Prognosen in Deutschland beruhen nicht auf Umfragen vor der Wahl, sondern auf exit polls. Bei einem der beiden Forschungsinstitute, die solche Prognosen erstellen, nämlich bei infratest-dimap, geschieht das so: Bei bundesweiten Wahlen werden mehrere hundert Wahlsprengel nach statistischen Kriterien ausgewählt (bei der letzten Bundestagswahl 640) und die Wähler in diesen Wahlsprengeln gebeten, auf einem Fragebogen ihre gerade getroffene Wahlentscheidung anzukreuzen sowie einige weitere Daten über sich zu machen (Geschlecht, Alter usw.). Diesen Fragebogen werfen sie dann selbst in eine Urne. Die Urne wird im Laufe des Tages mehrmals geleert und die jeweiligen Zwischenergebnisse an die Prognosezentrale übermittelt. Insgesamt wurden bei der letzten Bundestagswahl etwa 100.000 Wähler so befragt.
Diese Form der Prognose unterscheidet sich in wesentlichen Punkten von der bei der Gemeinderatswahl Wien verwendeten Methode.
In Deutschland
* werden wesentlich mehr Wähler befragt
* sind die Antworten erkennbar anonymisiert
* müssen sich die Wähler nicht an frühere Wahlentscheidungen erinnern
* werden die Befragten nicht vorab nach ihrer Wahlabsicht sondern unmittelbar nach ihrer Stimmabgabe nach ihrer Wahlentscheidung gefragt.
Dass ein derartiger großer exit poll deutlich zuverlässigere Resultate liefert als eine im Vergleich dazu kleine vor der Wahl durchgeführte Umfrage ist nicht besonders überraschend. Natürlich kostet ein derartiger exit poll auch ein Vielfaches einer telefonischen Vorwahlumfrage.
Es war eine ziemlich wagemutige Entscheidung von Fernsehanstalten, am Wahltag Wahlprognosen auf Grund von Umfragen vor der Wahl zu publizieren.
Bei der politischen Umfrageforschung gibt es sowieso Probleme, derer sich vor allem Statistiker schmerzlich bewusst sind.
Bei Umfragen werden mittlerweile (noch vor wenigen Jahren war das nicht so) Schwankungsbreiten publiziert. Die Schwankungsbreite beträgt bei einer 1000er-Umfrage ±3,16%, bei einer 400er-Umfrage ±5,0%. Auch wenn man sich keine Formeln merken mag gibts dafür eine Faustregel: Bei einer Umfrage mit 100 Befragten ist die Schwankungsbreite ±10,0%, und bei jeder Vervierfachung des Stichprobenumfangs wird die Schwankungsbreite halbiert. Die Voraussetzung für die Anwendung der dahintersteckenden Formel ist allerdings, dass es sich dabei um eine echte Zufallsstichprobe handelt und dass die Prozentsätze direkt aus den Rohdaten ohne irgendwelche Nachjustierungen errechnet werden. Beides ist typischerweise bei politischen Umfragen nicht der Fall. Telefonumfragen liefern aus verschiedenen Gründen keine klassischen Zufallsstichproben. Außerdem wird bei den Umfragen die Zahl der Antwortverweigerer meist nicht dokumentiert. Dadurch alleine ist meist die angegebene Schwankungsbreite schon irreführend, die sollte nämlich mit der Zahl derer, die eine auswertbare Antwort gegeben haben, berechnet werden, und nicht mir der Anzahl der Befragten. Wenn man nur die Prozentsätze der auswertbaren Antworten ausweist, dann geht man davon aus, dass das Ergebnis der Antwortverweigerer nicht systematisch anders wäre als das der Antworter. Dieses Problem versucht man mit „Kontrollfragen“ teilweise lösen. Man geht davon aus, dass man den statistischen Zusammenhang zwischen anderen Fragen und der Wahlentscheidungsfrage kennt, und versucht so, zumindest teilweise die verweigerten Antworten zur Wahlentscheidung zu extrapolieren.
Wenn man den Konsumenten von Meinungsumfragen dabei helfen will, die Qualität und Zuverlässigkeit der Umfragen einzuschätzen, dann sollte man
* die Methode der Stichprobenauswahl klar dokumentieren
* bei jeder Frage die Zahl der auswertbaren Antworten angeben
* zumindest Hinweise auf die Extrapolationsverfahren, mit denen verweigerte Antworten kompensiert werden, geben.
Man kann aus der schiefgegangenen Prognose aber auch etwas Grundsätzliches lernen: Umfragen sind ein durchaus taugliches Instrument zur Erhebung der momentanen Stimmungslage, als Prognoseinstrument taugen sie aber definitiv nicht. Die auf der Zufallsstichprobenmethodik beruhenden Formeln zur Berechnung der Schwankungsbreiten sind nämlich nicht anwendbar, weil die Voraussetzungen dafür bei den meisten Umfragen nicht erfüllt sind.

Noch etwas weiteres ist anzumerken: es scheint mir etwas naiv, zu glauben, dass man mit den Umfragen, die bezüglich der Wahlentscheidung definitiv ziemlich weit daneben gelegen sind, halbwegs präzise Aussagen das Wahlverhalten von Untergruppen von Wählern (beispielsweise der unter 30-jährigen Männer) ableiten kann. Diese Untergruppen sind nämlich viel kleiner als die gesamte Stichprobe (unter 30-jährige Männer sind etwa 10% der Wahlberechtigten), und daher sind die Stichprobenergebnisse auch viel ungenauer. Bei derartigen Aussagen nur die Schwankungsbreite anzugeben wäre sogar dann grob verfälschend, wenn es sich um eine klassische Zufallsstichprobe handelte.

Und noch eine Anmerkung scheint mir wichtig. Am Wahlabend wurde bereits eine Wählerstromanalyse publiziert, die den Anspruch stellt, alle Wählerströme zu erfassen. Bei dieser Wahl wurden allerdings etwas 20% der Stimmen mit Wahlkarten abgegeben, und die meisten davon waren am Wahlabend noch nicht ausgezählt. Die Wählerstromanalyse beruht also bei einem wesentlichen Anteil der Stimmen auf einer Trendextrapolation für die Wahlkartenstimmen und nicht auf einer Analyse sämtlicher ausgezählter Stimmen. Man sollte also diese Analyse auch mit entsprechender Vorsicht interpretieren. Redlicher erschiene mir, eine Wählerstromanalyse nur mit den ausgezählten Stimmen und zusätzlich eine Variante mit den extrapolierten Wahlkartenstimmenergebnissen zu publizieren.

Auch zu den vielen und in vielen Fällen sehr informativen Landkarten, die auf den Sprengelergebnissen beruhen, ist anzumerken, dass die Sprengelergebnisse keine Wahlkartenstimmen umfassen. Schlussfolgerungen wie „in den Außenbezirken war die Wahlbeteiligung höher als in den Innenbezirken“ können durch verschieden hohe Wahlkartenstimmenanteile systematisch verzerrt werden.

Statistik besteht nicht nur darin, Formeln zu verwenden oder Grafiken aus Daten zu erstellen. Statistik muss auch überlegen, ob die vorhandenen Daten genau jene Struktur haben, die man zum Beantworten der interessierenden Fragen braucht. Interpretationen feinkörniger Wahlergebnisse, bei denen Wahlkartenstimmen nicht so einfach eingerechten werden können, können durchaus auch verfälschte Bilder vermitteln. Und in Wählerstromanalysen, die die Wahlkartenstimmen noch schätzen (müssen), weil sie noch fehlen, gehen subjektive Annahmen der Analysierenden und nicht nur objektiv ermittelte Daten ein. Das ist durchaus zulässig, sollte aber sehr klar erkennbar gemacht werden. Und Fernsehanstalten sollten sich genau überlegen, ob sie wirklich am Wahltag Umfragen als Prognoseinstrumente einsetzen wollen. Wenn sie das wollen, dann sollten sich auch ernsthaft mit Fachleuten darüber reden, mit welcher Methode sich welche Prognosegenauigkeit erreichen lässt.

Statistisches zum EU-Austritts-Volksbegehren

Heute habe ich in der nzz.at eine Wahlanalyse des Wahlanalyse des EU-Austritts-Volksbegehrens publiziert.

Eine etwas detailliertere gibt es auf meiner neuen Website www.wahlanalyse.com

Es gibt auch eine klickbare Landkarte mit den Gemeindeergebnissen und eine klickbare Landkarte mit den Bezirksergebnisse.

Diese Landkarten funktioneren auf iPads und iPhones leider derzeit nicht.

Ich hab auch schon vor einiger Zeit zu dem Thema geblogged.

Warum gibt es zwei Analysen?

Es geht um statistische Grafiken. Ich verwende in meinen Analysen gerne Boxplots. Ich versuche auch immer wieder, diese Darstellungsform in Zeitungsartikeln zu verwenden. Bisher bin ich aber immer gescheitert. Die Redakteure sind nämlich der Meinung, dass diese Art von Grafik für die Leser nicht verständlich genug ist.

Mittlerweile sind Boxplots Mathematikstoff der 4. Klasse AHS. (siehe etwa dieses Schulbuch).

Es besteht also die Hoffnung, dass in einigen Jahren auch Tageszeitungen, die sich als Qualitätsmedien verstehen, diese Grafikform in Artikeln zulassen.

Vielleicht sollte ich eine Erklär-Video im Stile der Sendung mit der Maus machen.

Ökonomen und der Nobelpreis

In der Presse gibts einen Artikel, in dem über den Einfluss von US-Ökonomen auf die öffentliche Diskussion über die Probleme Griechenlands gesprochen wird. Die Presse schreibt, dass die Tatsache, dass es sich um „Nobelpreisträger“ handelt, den Argumenten besonderes Gewicht gegeben hat.

Zum Thema Ökonomie und Nobelpreis hab ich vor circa 3 Jahren einen Artikel im standard geschrieben.

Ich hab mit meinen dort geäußerten Befürchtungen leider recht behalten.

Eine kurze (etwas vereinfachende) Zusammenfassung dieses Artikels:

Es gibt keinen Nobelpreis für Ökonomie. Nobelpreise sind von Alfred Nobel gestiftete Preise. Die Spielregeln für diese Preise hat Alfred Nobel in seinem Testament festgelegt.

Diese Preise gibt es seit 1901.

1968 hat die Schwedische Reichsbank einen Alfred-Nobel-Gedächtnispreis für Wirtschaftswissenschaften gestiftet. Die Spielregeln hat in Anlehnung an die Nobelpreise die Reichsbank – also Ökonomen – festgelegt.

Verkürzend und verfälschend sprechen viele Leute – vor allem in dieversen Medien – da von einem Nobelpreis für Wirtschaftswissenschaften. Und schreiben den Äußerungen von Preisträgern ein wohl zu hohes Gewicht zu.

Die Ökonomen versuchen da meiner Meinung nach, als Trittbrettfahrer am Renommee eines Preises für andere Wissenschaften zu partizipieren.

EU-Austritts-Volksbegehren – regionale Unterschiede

Am 1. Juli ist die Frist zur Unterzeichnung des EU-Austritts-Volksbegehrens zu Ende gegangen. Derzeit gibts auswertbar die Ergebnisse der Bezirke. Gemeindeergebnisse, die man für detaillierte statistische Analysen braucht, wird es erst später geben.

Berteits mit den Bezirksergebnissen kann man eine (interaktive, klickbare) statistische Landkarte erstellen.

Achtung: Die Datenmenge der Karte ist relativ groß und benötigt einiges an Ressourcen. Auf manchen mobilen Geräten kann es daher zu Schwierigkeiten bei der Darstellung kommen.

Dieser Typ von statistischer Landkarte heißt übrigens Choroplethenkarte.