Das Assoziativgesetz – was ist das und warum ist das wichtig?

Im Mathematikunterricht lernt man

$$(a+b)+c=a+(b+c)$$

Das ist das Assoziativgesetz.

Als Zeichenkette aus Buchstaben und mathematischen Zeichen ist das nicht besonders beeindruckend, und man sieht auch nicht, warum das wichtig ist.

Praktisch verwendet man es oft, ohne dass man es merkt.

Wenn man beispielsweise $25+27+23$ berechnen soll, dann kann man zuerst $25+27=52$ berechnen und dann $52+23=75$ berechnen, um das Ergebnis zu erhalten. Man kann aber auch „sehen“, dass $27+23=50$ ist, und braucht dann nur $25+50=75$ zu berechnen. Die zweite Art der Berechnung ist „handlicher“, und das Assoziativgesetz ist der Grund, dass wir sicher sein können, bei beiden Rechnungen dasselbe Ergebnis zu erhalten.

Man kann das Assoziativgesetz auch sehr anschaulich illustrieren.
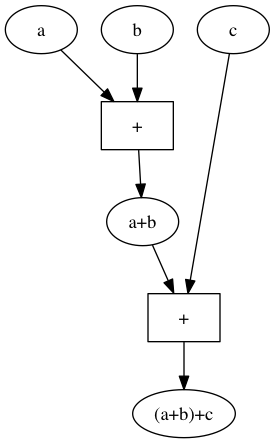
Wenn man $(a+b)+c$ als grafische Rechenmaschine darstellt sieht das so aus:

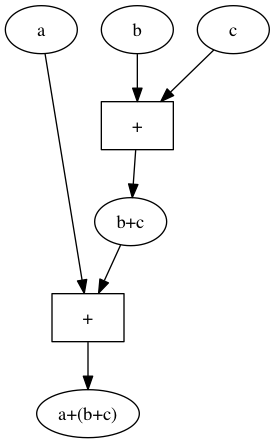
Die grafische Darstellung von $a+(b+c)$ sieht so aus:

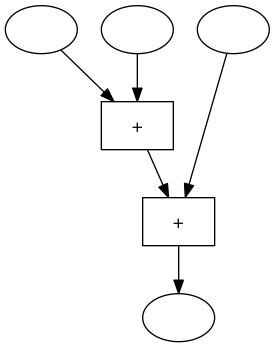
Wir können diese beiden „Rechenmaschinen“ auch ohne die Variablennamen veranschaulichen. Jede dieser Maschinen hat 3 Inputs und einen ouput. Im Inneren der Maschine gibt es 2 Addierwerke. Die erste Maschine addiert den ersten und den zweiten Input und addiert dann zu dieser Summe den dritten Input.

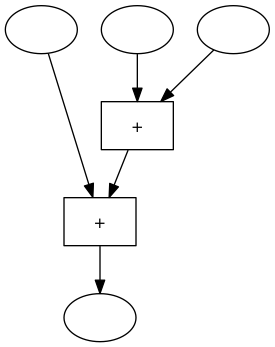
Die zweite Rechenmaschine addiert zuerst den zweiten und den dritten Input und addiert dann zu dieser Summe den ersten Input:

Die Rechenwerke in diesen Maschinen sind verschieden verdrahtet, aber wir wissen, dass beide Maschinen bei gleichen Inputs immer dasselbe Ergebnis liefern.

Wir können das dazu verwenden, andere Maschinen, in denen diese 3er-Addiermaschine als Teil vorkommt, umzubauen.

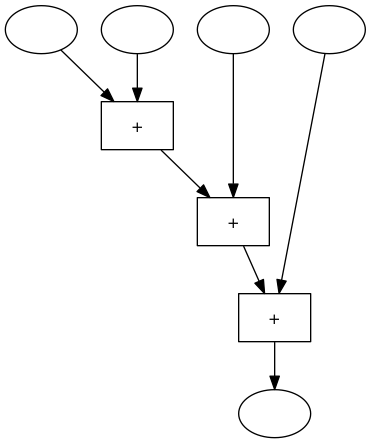
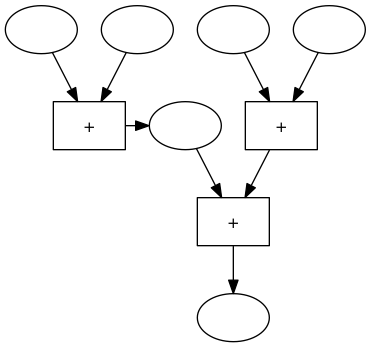
Eine einfache Maschine zum Addieren von 4 Zahlen sieht so aus:

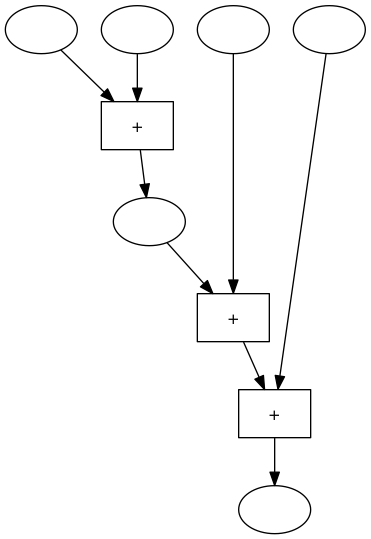
Wir markieren in dieser Maschine ein Zwischenergebnis mit einem Oval

und wir verschieben die Blöcke in der Maschine ein bisschen

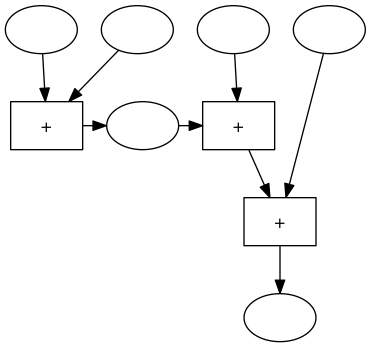
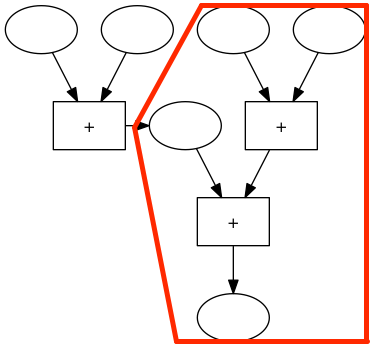
Im rechten Teil diese Maschine gibt es einer 3er-Addiermaschine:

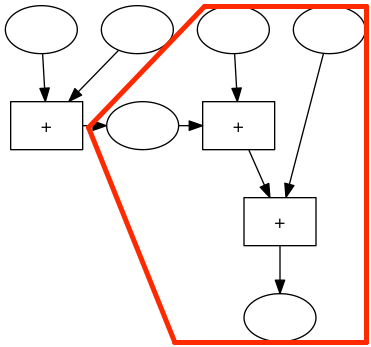
Diese Maschine können wir durch eine andere 3er-Addiermaschiene, die immer dasselbe Ergebnis liefert, ersetzen:

In dieser Maschine

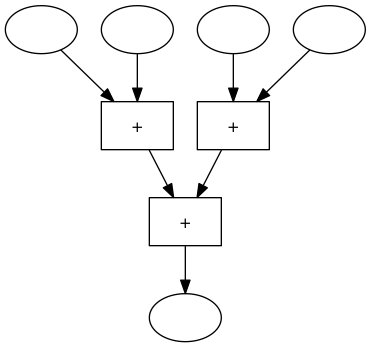
können wir den Block für das Zwischenergebnis wieder entfernen und die Blöcke noch etwas verschieben und erhalten dann folgende Maschine:

Und wozu das ganze?

In der usprünglichen 4er-Addiermaschine mussten 2 der 3 Rechenwerke auf das Ergebnis des vorgeschalteten Rechenwerks warten. In der neuen 4er-Addiermaschine können 2 Rechenoperationen gleichzeitig durchgeführt werden. Die erste Maschine braucht also 3 Zeiteinheiten für das Addieren von 4 Zahlen, die zweite Maschine braucht nur 2 Zeitschritte, sie kann also schneller rechnen.

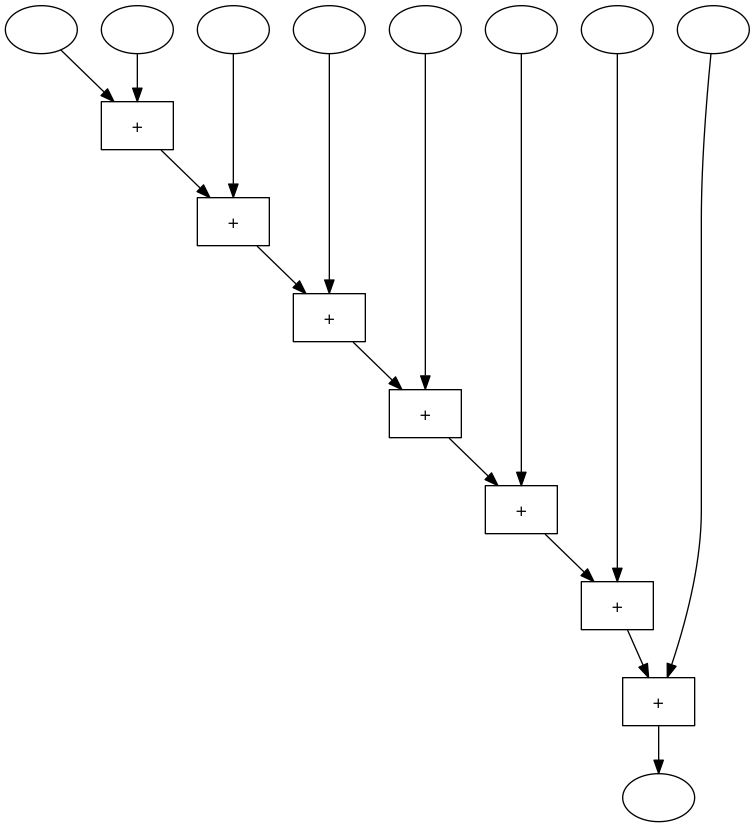
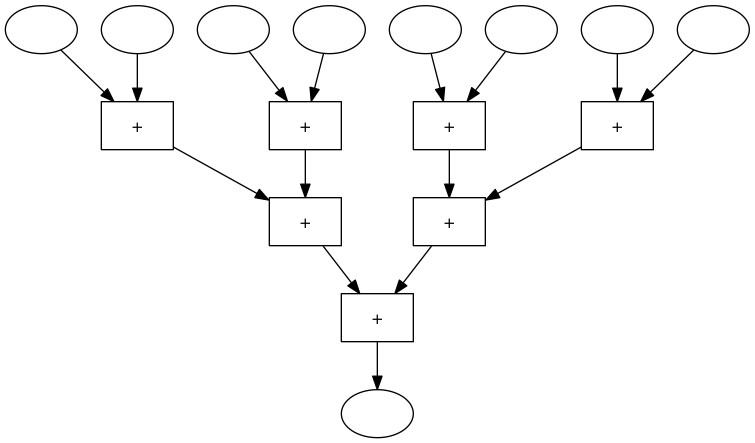
Eine 8er-Addiermaschine die immer eine Zahl zur vorherigen Summe addiert, sieht so aus:

Wenn man in dieser Maschine merhmals 3er-Maschinen durch funktionsgleiche 3er-Maschinen ersetzt, dann erhält man folgende Maschine:

Die ursprüngliche 8er-Maschine brauch 7 Zeitschritte, die umgebaute Maschine nur 3.

Das Umbauen der Maschine funktioniert nur, weil das Assoziativgesetz gilt.

Geschicktes Anwenden dieses Gesetzes führ also dazu, dass man bei bestimmten Aufgaben wesentlich schneller Rechnen kann.

Parallele Computerarchitektur ist eine der neuen Entwicklungen der Computertechnik. Was wir hier beschrieben haben ist eines der Prinzipien, nach denen parallele Programme arbeiten.