Ein #mathepuzzle
und was man daraus alles lernen kann
Ich poste (als @neuwirthe) auf Twitter regelmäßig mathematische Puzzles unter den hashtag #mathepuzzle. Unlängst hab ich folgendes gepostet: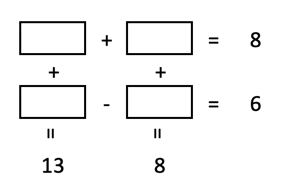
Viele Leser haben die richtige Lösung gefunden. Wie kann man die Lösung intelligent suchen?
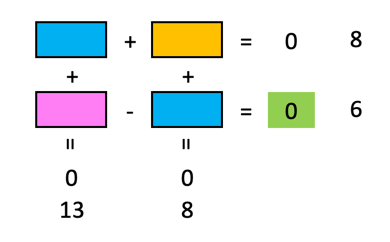
In beiden Zellen können wir daher die Formel „8 – orange Zelle” eingeben.
In der lila Zelle kommt die Formel „13 – blaue Zelle darüber“.
Wenn wir das machen, dann erhalten wir Folgendes:
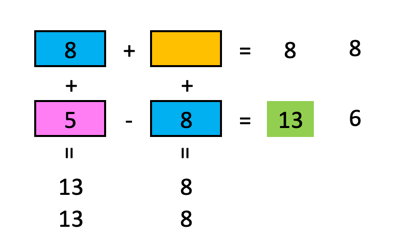
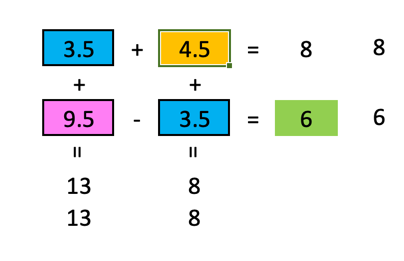
Dann muss in den beiden blauen Feldern $8-x$ stehen.
Im lila Feld steht dann $13-(8-x)=5+x$. Der Wert im grünen Summenfeld ist daher $(5+x)-(8-x)=2x-3$. Dieser Wert soll 6 sein, also lautet die Gleichung, die wir lösen müssen, $2x-3=6$ und die Lösung ist $x=\frac{9}{2}=4.5$. Wir können dieses Beispiel auch mit Mitteln der (etwas) höheren Mathematik angehen 😉
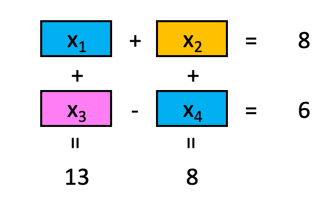
\begin{split}
&1 x_1 + 1 x_2 + 0 x_3 &+ &0 x_4 &= 8 \\
&0 x_1 + 0 x_2 + 1 x_3 &- &1 x_4 &= 6 \\
&1 x_1 + 0 x_2 + 1 x_3 & + &0 x_4 &= 13 \\
&0 x_1 + 1 x_2 + 0 x_3 & + &1 x_4 &= 8
\end{split}
$$
Diese Schreibweise alleine hilft noch nicht, mehr herauszufinden. In der Mathematik gibts noch eine Kurzschreibweise, die es uns erspart, die Variablen so oft anzuschreiben: $$
\begin{pmatrix}
1 & 1 & 0 & 0 \\
0 & 0 & 1 & -1 \\
1 & 0 & 1 & 0 \\
0 & 1 & 0 & 1
\end{pmatrix}
\begin{pmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix}
=
\begin{pmatrix} 8 \\ 6 \\ 13 \\ 8 \end{pmatrix}
$$ In der Mathematik gibt es Hilfsmittel, zu entscheiden, ob ein derartiges Gleichungssystem immer lösbar ist, auch dann, wenn man die Zahlen auf den rechten Seite der Gleichungszeichen beliebig ändert.
Wenn wir das entsprechend aufschreiben sieht es so aus:
$$
\begin{pmatrix}
1 & 1 & 0 & 0 \\
0 & 0 & 1 & -1 \\
1 & 0 & 1 & 0 \\
0 & 1 & 0 & 1
\end{pmatrix}
\begin{pmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix}
=
\begin{pmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \end{pmatrix}
$$ Mit mathematischen Hilfsmitteln erhalten wir dann für beliebige rechte Seiten die Lösung $$
\frac{1}{2}\begin{pmatrix}
1 & 1 & -1 & -1 \\
0 & -1 & 1 & 1 \\
-1 & 1 & 1 & 1 \\
-1 & 1 & 1 & -1
\end{pmatrix}
\begin{pmatrix}r_1 \\ r_2 \\ r_3 \\ r_4 \end{pmatrix}
=
\begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix}
$$ Wenn wir unsere Zeilen- und Spaltensumme $r_1=8$, $r_2=6$, $r_3=13$ und $r_4=6$ einsetzten dann erhalten wir die Lösung $x_1=\frac{7}{2}$, $x_2=\frac{9}{2}$, $x_3=\frac{19}{2}$ und $x_4=\frac{7}{2}$. Der Zweig der Mathematik, der Lösbarkeit und Lösungsmethoden solcher Gleichungssysteme untersucht, heißt Lineare Algebra.
Wir können solche Gleichungssystem in vielen speziellen Fällen lösen. Das Wissen, dass unser Puzzle bei beliebigen Zeilen- und Spaltensummen immer eindeutig lösbar ist, liefern aber erst die Methoden der Linearen Algebra.