Hochrechnungen ohne offizielle Gemeindeergebnisse – geht das?
Man hört und liest gerade, dass es Pläne gibt, bei der EU-Wahl schon vor der offiziellen Bekanntgabe der Ergebnisse durch das BMI Hochrechnungen zu machen. Die Daten dazu sollen Wahlzeugen an eine zentrale Plattform melden.
Wahlzeugen sind von den Parteien nominierte Personen, die in den einzelnen Wahlsprengeln den Wahlvorgang und die Auszählung beobachten dürfen, und daher die Sprengelergebnisse „ihres“ Sprengels sofort nach Ende der Auszählung kennen.
Im Gegensatz zu den Wahlbeisitzern unterliegen Wahlzeugen aber nicht der Amtsverschwiegenheit.
Ich habe bei einer derartigen Beschaffungsaktion von Sprengelergebnissen einige Bedenken.
- Bei Hochrechnungen braucht man Ergebnisse gleicher regionaler Einheiten von einer (früheren) Vergleichswahl. Sprengelergebnisse werden aber nicht zentral gesammelt, man hat also Sprengelergebnisse früherer Wahlen nur in großen Städten, die das selber als Daten gesammelt zur Verfügung stellen. Für Gemeinden mit mehreren Sprengeln gibt es das in der Regel nicht. Und sicherstellen, dass man alle Sprengel einer Gemeinde bekommt, ist ziemlich aufwändig.
- Es gibt bei dieser eher informellen Art der Übermittlung sicher nicht dieselbe Qualitätssicherheit wie wenn man die gesammelten Daten des BMI bekäme.
- Gute Qualitätssicherung erscheint mir bei einem derartigen Projekt ziemlich aufwändig. Wahlzeugen werden von den politischen Parteien nominiert. Man macht sich also bei der Datenbeschaffung bereits von Parteien abhängig. Das halte ich bei Wahlen für nicht sehr wünschenswert.
Mandatszuteilung nach D’Hondt
Spielereien mit dem EU-Wahl-2014-Ergebnis
Bei der EU-Wahl 2014 wurden 18 Mandate vergeben.
| ÖVP | SPÖ | FPÖ | GRÜNE | NEOS | |
|---|---|---|---|---|---|
| 5 | 5 | 4 | 3 | 1 |
Das Verfahren, mit dem die Mandate aus den Stimmen errechnet werden, ist das Verfahren nach d’Hondt.
Wie funktioniert das?
Die übliche Beschreibung ist relativ kompliziert, und man versteht meist nicht, wie sie zustandekommt.
Das Prinzip dahinter ist einfach: Bestimme die größtmögliche Wahlzahl, mit der du noch alle Mandate vergeben kannst und verteile dann die Mandate mit dieser Wahlzahl.
Da stellt sich die Frage: Was ist eine Wahlzahl?
Eine Wahlzahl legt fest, für wieviele Stimmen eine Partei ein Mandat bekommt.
Ist die Wahlzahl 150.000, dann bekommt eine Partei mit weniger als 150.000 Stimmen kein Mandat,
mit 150.000 bis 299.999 Stimmen ein Mandat, mit 300.000 bis 449.999 Stimmen 2 Mandate usw.
Eine Partei mit 350.000 Stimmen bekommt demnach (bei einer Wahlzahl vom 150.000) 2 Mandate und hat 50.000 unverbrauchte Stimmen.
Diese Stimmen heißen auch Reststimmen.
Wenn man die Wahlzahl kennt, dann
dividiert man nach diesem Varfahren zunächst die Stimmenzahlen der Parteien durch die Wahlzahl. Dieser Quotient (also das Divisionsergebnis) ist in den meisten Fällen keine ganze Zahl. Das Divisionergebnis wird dann abgerundet und die abgerundete (ganze) Zahl ist die Zahl von Mandaten, die der betreffenden Partei zugewiesen werden. Zieht man von der Stimmenzahl der Partei das Produkt der Wahlzahl mit der Mandatszahl ab, dann ist diese Differenz die Zahl der Reststimmen.
Die Stimmenzahlen der Parteien bei der EU-Wahl 2014 waren
| ÖVP | SPÖ | FPÖ | GRÜNE | NEOS | |
|---|---|---|---|---|---|
| 761896 | 680180 | 556835 | 410089 | 229781 |
Bei einer Wahlzahl von 200.000 wäre die Mandatsverteilung
| ÖVP | SPÖ | FPÖ | GRÜNE | NEOS | |
|---|---|---|---|---|---|
| 3 | 3 | 2 | 2 | 1 |
Es würden also (bei einer Wahlzahl von 200.000) insgesamt 11 Mandate vergeben.
Bei einer Wahlzahl von 100.000 wäre die Mandatsverteilung
| ÖVP | SPÖ | FPÖ | GRÜNE | NEOS | |
|---|---|---|---|---|---|
| 7 | 6 | 5 | 4 | 2 |
Es also würde (bei einer Wahlzahl von 100.000) insgesamt 24 Mandate vergeben.
Bei der EU-Wahl 2014 mussten genau 18 Mandate vergeben werden.
Wie findet man eine Wahlzahl, bei der man genau eine vorgegebene Zahl von Mandaten vergeben kann?
Durch Herumprobieren kann man herausfinden, dass 130.000 als Wahlzahl „funktioniert“, mit dieser Wahlzahl werden genau 18 Mandate vergeben.
Anmerkung: Einmal in die Tabelle klicken lässt den Erläuterungstext über Cookies verschwinden und zeigt die ganze Tabelle.
Mit der Wahlzahl 130.000 kann man alle 18 Mandate vergeben. Allen Parteien bleiben Reststimmen, also kann man mit einer etwas größeren Wahlzahl (z.B. 131.000) auch noch alle Mandate vergeben.
Auch bei Wahlzahlen von 135.000 und 136.000 werden genau 18 Mandate vergeben.
Bei eine Wahlzahl von 136.500 werden aber nur mehr 17 Mandate vergeben.
Also liegt zwischen 136.000 und 136.500 die größte Wahlzahl, bei der gerade noch 18 Mandate vergeben werden.
Wie können wir die finden?
Bei einer Wahlzahl vom 136.000 bleiben der SPÖ nur mehr wenige Reststimmen, nämlich 180.
Wie hoch kann denn die Wahlzahl werden, damit der SPÖ genau 0 Reststimmen bleiben.
Klarerweise ist das bei einer Wahlzahl von $\frac{680.180}{5}=136.036$ der Fall.
Wenn die Wahlzahl genau ein Fünftel der Stimmen der SPÖ ist, dann ergibt die Division Stimmenzahl durch Wahlzahl genau 5 und es bleiben keine Reststimmen. Sobald die Wahlzahl nur ganz wenig größer wäre, ergäbe die Division nur mehr 4 Mandate.
Wenn wir also möglichst wenig Restimmen haben wollen, dann erreichen wir das, wenn eine Partei 0 Reststimmen hat, und das ist dann der Fall, wenn die Stimmenzahl einer Partei ganz genau ein Vielfaches der Wahlzahl ist oder – anders gesagt – die Wahlzahl der Quotient der Stimmenzahl einer Partei und einer ganzen Zahl (der Mandatszahl dieser Partei) ist. Wenn wir also für alle Parteien folgende Zahlen berechnen: Stimmenzahl, Stimmenzahl/2, Stimmenzahl/3, Stimmenzahl/4, ….. Stimmenzahl/Gesamtmandatszahl, dann ist die Wahlzahl eine dieser Zahlen. Wir werfen alle diese Zahlen „in einen Topf“, sortieren sie (absteigend) der Größe nach und nennen diese Zahlenreihen Quotientenreihe.
Sind 2 Mandate zu vergeben, dann gibt es 2 Möglichkeiten: die stärkste Partei bekommt alle beiden Mandate oder die beiden stärksten Parteien bekommen je ein Mandat.
Wann bekommt die stärkste Partei beide Mandate? Wenn sie mehr als doppelt so viele Stimmen als die zweitstärkste Partei hat, dann funktionierte die Hälfte ihrer Stimmen als Wahlzahl. Alle anderen Parteien haben weniger Stimmen als diese Wahlzahl, daher bekommen die anderen Parteien keine Mandate und die stärkste Partei bekommt 2 Mandate. Hat die zweitstärkste Partei mehr als die Hälfte der Stimmen der ersten Partei, dann funktioniert ihre Stimmenzahl als Wahlzahl. Sie bekommt 1 Mandat, und der Quotient der Stimmen der stärksten und der zweitstärksten Partei ist kleiner als 2 (die stärkste Partei hat weniger als doppelt so viel Stimmen wie die erste Partei), also bekommt die stärkste Partei auch nur ein Mandat.
In beiden möglichen Fällen ist also die zweitgrößte Zahl aus der Quotientenreihe die Wahlzahl.
Wenn 3 Mandate zu vergeben sind, dann kommen nur die 3 stimmenstärksten Parteien für ein Mandat in Frage. Es gibt dann 3 Möglichkeiten der Aufteilung: 3/0/0, 2/1/0 und 1/1/1.
Hat die stärkste Partei mehr als 3x so viele Stimmen als jede der beiden anderen Parteien, dann funktioniert 1/3 der Stimmen dieser Partei als Wahlzahl. Beide anderen Parteien haben dann weniger Stimmen als die Wahlzahl, die Division der Stimmen der stärksten Partei durch die Wahlzahl geht sich genau aus und die stärkste Partei bekommt alle 3 Mandate.
Hat die stärkste Partei mehr als doppelt so viele Stimmen als die zweitstärkste (und daher auch die drittstärkste) Partei, aber weniger als 3x so viele Stimmen, dann funktioniert die Stimmenzahl der zweitstärksten Partei als Wahlzahl. Die Division der Stimmenzahl der stärksten Partei durch diese Wahlzahl ergibt eine Zahl zwischen 2 und 3, daher erhält diese Partei 2 Mandate. Die zweitstärkste Partei erhält (ihre Stimmenzahl ist ja die Wahlzahl) genau ein Mandat.
Ist die Stimmenzahl der stärksten Partei kleiner als die doppelte Stimmenzahl der zweitstärksten, dann hängt das Mandatsergebnis von der Stimmenzahl der drittstärksten Partei ab. Ist die Stimmenzahl der stärksten Partei größer als das Doppelte der Stimmenzahl der drittstärksten Partei, dann funktioniert die Hälfte der Stimmenzahl der stärksten Partei als Wahlzahl. Die stärkste Partei bekommt 2 Mandate, die zweitstärkste 1, und die drittstärkste (ihre Stimmenzahl ist ja geringer als die Wahlzahl) kein Mandat.
In allen Fällen ist die Wahlzahl die dritte Zahl in der Quotientenreihe.
Beispiel:
Bei einer Stimmenverteilung von 90000/50000/40000 ergibt die Wahlzahl 45000 eine Mandatsverteilung von 2/1/0.
Bei einer Stimmenverteilung von 90000/50000/48000 ergibt die Wahlzahl 48000 eine Mandatsverteilung von 1/1/1.
Diese Überlegungen kann man für höhere Mandatszahlen mathematisch formalisieren. Der Algorithmus zur Mandatsvergabe lautet dann:
Man bilde die Quotientenreihe und verwende die Zahl, die an der Stelle steht, die der Zahl der zu vergebenden Mandate entspricht, als Wahlzahl.
In der folgenden Tabelle können sie die Zahlen in den gelb markierten Zellen ändern und so verschiedene Szenarien ausprobieren.
Es kann passieren, dass 2 oder mehr Parteien gleichen Anspruch auf ein Mandate haben.
Ein Beispiel: Partei A hat 100.000 Stimmen, Partei B und Partei C je genau 50.000 Stimmen und es sind 3 Mandate zu vergeben.
Dann ist die drittgrößte Zahl in der Quotientenreihe 50.000, die viertgrößte aber ebenfalls. In so einem Fall wird meist durch das Los entschieden, wer das strittige Mandat erhält.
Zum Download gibts eine Excel-Arbeitsmappe mit dem d’Hondt’schen Verfahren für das Ergebnis der EU-Wahl 2014. Man kann dort auch die Stimmenzahlen verändern und die Auswirkungen auf das Mandatsergebnis beobachten.
Man kann in dieser Arbeitsmappe z.B. nachprüfen, dass die Grünen mit 30.000 Stimmen weniger 1 Mandat weniger bekommen
hätten (das Mandat wäre zur ÖVP gewandert).
Die ÖVP hatte mit 60.000 1 Mandat mehr (auf Kosten der SPÖ) bekommen.
Mathematische Erklärung
Dieser Abschnitt wendet sich nur an Leser, die einigermaßen fließend im Decodieren und Übersetzen der algebraischen Schreibweise sind.
$S_i$ mit $i=1\ldots k$ seien die Stimmen der Partei $i$
$q_{i,j}=\frac{S_i}{j}$ seien die Folge der Parteienquotienten.
$q_{(h)}$ seien die „zusammengelegten und der Größe nach geordneten” Parteienquotienten, es sei also $q_{(1)}$ der größte aller Parteienquotienten, $q_{(2)}$ der zweitgrößte usw. Wir nennen sie Gesamtquotientenreihe.
Wir nehmen an, dass alle Quotienten voneinander verschieden sind.
$w$ sei einer der Parteienquotienten, und zwar $w=\frac{S_I}{m_I}$. Wir suchen für alle Parteien $i$ jenes $m_i$ für das $\frac{S_i}{m_i} \gt w$ und $\frac{S_i}{m_i+1} \lt w$.
Ausnahme: Für $i=I$ sei $m_I$ die Zahl mit $\frac{S_I}{m_I}=w$.
$M$ sei die Summe dieser $m_i$, $M=\sum_{i=1}^{k}m_i$
Dann gilt für $j=1\ldots m_i$ die Ungleichung $\frac{S_i}{j} \geq w$ und weiters gilt $\frac{S_i}{m_i+1} \lt w$
Das ist äquivalent mit $m_i w \leq S_i$ und $(m_i+1) w \gt S_i$
In der Sprache der Wahlarithmetik bedeutet das, dass bei einer Wahlzahl $w$ die Partei $i$ mit $S_i$ Stimmen $m_i$ Mandate erhält und dass insgesamte $M$ Mandate vergeben werden.
Für alle $i$ und $j \le m_i$ gilt $q_{i,j} \geq w$, und es gibt $M$ dieser Parteiquotienten. Die sind gleichzeitig auch die $M$ größten $q_{(h)}$ und es gilt $q_{(h)}\geq w$ für $h \leq M$. Daher ist $w$ die $M$-größte Zahl in der Gesamtquotientenreihe.
Michel Reimon und die Straßenbahn
Michel Reimon (@michelreimon) hat auf Twitter folgendes gepostet:Du wohnst 3 min Fußweg von der Haltestelle entfernt. Die Straßenbahn fährt alle 5 Minuten. In 60% der Fälle fährt dir also eine Bim vor der Nase davon. Und da sollst du nicht frustriert werden???Diese Überlegung ist aber nur teilweise richtig. Nehmen wir an die Straßenbahn fährt zum x:00, x:05, x:10 usw. ab. Und nehmen wir auch an, dass Michel Reimon mit „fährt vor der Nase davon“ meint, dass man auf dem Weg zur Station von einer Straßenbahn überholt wird. Sehen wir uns dann die Situation in einen Zeit-Weg-Diagramm an: Die Grafik zeigt die Zeit-Weg-Diagramme des Fußgehers und mehrerer Straßenbahnen. Die x-Achse ist die Zeit, die y-Achse die Strecke. Die Einheit auf der x-Achse sind Minuten, die Einheit auf der y-Achse die Strecke, die der Fußgeher in 1 Minute zurücklegt. Der Fußgeher wird von einer Straßenbahn überholt, wenn die Fußgeherlinie (schwarz) eine Straßenbahnlinie (rot) schneidet. Der Punkt Abfahrt (blau) ist (waagrecht) verschiebbar, man kann das also in der Grafik ausprobieren. Es ist klar, dass der Fußgeher nicht überholt wird, wenn er genau zum Zeitpunk 0 (da fährt Straßenbahn 1 von der Station weg) vom Wohnhaus losgeht. Das passiert auch, wenn er irgendwann zwischen Minute 0 und Minute 2 losgeht. Ist der Abmarsch später als zu Minute 2, dann schneiden einander die Fußgeherlinie und die Straßenbahnlinie 2, da überholt also Straßenbahn 2 den Fußgeher. Das wäre dann von Minute 2 bis Minute 5 und so kommt Michel Reimon vermutlich zu den 60%. Allerdings kommt da noch die Geschwindigkeit der Straßenbahn ins Spiel. Mit dem roten Punkt „Geschwindigkeitsfaktor Straßenbahn“ kann man einstellen, um wieviel schneller die Straßenbahn als der Fußgeher ist. Hier ist das zunächst auf einen Faktor 3 eingestellt, also so, dass die Straßenbahn 3x so schnell wie der Fußgeher ist. Verschiebt man den Abmarsch auf einen Zeitpunkt zwischen Minute 4 und Minute 5, dann überholt die Straßenbahn den Fußgeher aber nicht mehr. Also geht das Überholzeitfenster von Minute 2 bis Minute 4, das sind nur 40% der gesamten Zeit. Wenn die Straßenbahn mehr als 3x so schnell ist wie der Fußgeher, dann ändert sich diese Zeitspanne. Der rote Teil der Zeitachse zeigt Abmarschzeitpunkte, bei denen man von der Straßenbahn überholt wird, bei Abmarsch in blauen Zeitraum wird man von keiner Straßenbahn überholt. Das Problem geht übrigens davon aus, dass die Straßenbahn, die der Fußgeher erreichen will, in die Gehrichtung des Fußgehers fährt. Wäre es die Gegenrichtung, dann würden die Zeit-Weg-Diagramme etwas anders aussehen. Das Ermitteln der Formel für diesen Effekt bleibt jetzt dem User überlassen 😉 Stephan Fickl (@StephanFickl) hat mich auf Twitter zu Recht darauf hingewiesen, dass in meinem ersten Modell die Aufenthaltszeit der Straßenbahn in der Haltestelle nicht berücksichtigt ist. Daher habe ich noch ein erweitertes Modell erstellt, das die Stehzeiten berücksichtigt. Mit den verschiebbaren Punkten kann man Gehgeschwindigkeit, Fahrgeschwindigkeit, Ankunftszeit der Straßenbahn in der Haltestelle und Abmarschzeitpunkt einstellen. Außerdem wurde die y-Achse in Meter skaliert. Die in diese Seiten eingebetteten Applets wurden mit GeoGebra erstellt. GeoGebra ist ein (mit internationalen Preisen) ausgezeichnetes Programm für Mathematik. Die Entwicklergruppe (geleitet von Univ.Prof. Markus Hohenwarter) ist an der Universität Linz angesiedelt.
Infektionskrankheiten, Herdenimmunität und ein bisschen Mathematik
Welcher Prozentsatz einer Bevölkerung muss geimpft sein, damit sich eine Infektionskrankheit nicht epidemisch ausbreitet? Da kann ein wenig einfache Mathematik weiterhelfen.Wir nehmen vereinfachend auch an, dass jede(r) Erkrankte wieder gesund wird, danach gegen die Krankheit immun ist und auch niemand anderen mehr anstecken kann.
Ein Beispiel: Nehmen wir an niemand ist immun (geimpft) und ein bereits Infizierter steckt im Schnitt 5 weitere (nicht immune) Personen an. Die 5 stecken dann weiter 25 Personen an usw.
Wenn von den 5 aber 4 immun sind, dann erkrankt nur eine weitere Person und die Zahl der Infizierten „explodiert“ nicht. Bei einem Ansteckungsfaktor von 5 muss also ein Anteil von (1-1/5) der Bevölkerung geimpft sein, damit keine Epidemie ausbricht. Allgemeiner muss bei einer Ansteckungsrate von R ein Anteil von (1-1/R) der Bevölkerung geimpft sein, damit die Krankheit sich nicht zu sehr ausbreitet. Die Durchimpfungsrate, die man zur Epidemievermeidung braucht, ist bei einem Ansteckungsfaktor R also (1-1/R).
Schätzwerte für den Ansteckungsfaktor verschiedener Krankeiten lauten:
Pocken 3 bis 5
Masern 16 bis 18
Bei Masern brauchen wir (diesen Zahlen folgend) eine Durchimpfungsrate
von (1-1/18) ≃ 95% um Epidemien zu vermeiden. Dieses Rechenmodell ist natürlich grob vereinfachend, es bietet aber die Möglichkeit, zumindest grob abzuschätzen, welche Durchimpfungsraten bei verschiedenen Krankheiten zur Epidemievermeidung notwendig wären. Etwas mehr Mathematik dazu gibt es (auf Englisch) hier.
Wieviele 6-stellige Zahlen kann man mit 4 Ziffern schreiben?
Ein bisschen kombinatorisches Denken
Ich habe unlängst in meiner Twitterserie #mathepuzzle folgende Aufgabe gestellt:132324 ist eine 6-stellige Zahl, in der nur 4 verschiedene Ziffern vorkommen. Nennen wir so etwas eine 6-stellig 4-ziffrige Zahl. Wieviele 6-stellige 1-ziffrige, 2-ziffrige, …, 5-ziffrige und 6-ziffrige Zahlen gibt es? Führende Nullen sind erlaubt.Wie kann man das herausfinden? Mathematiker neigen dazu, solche Probleme gleich allgemeiner anzugehen. Überlegen wir also, welche verwandten Fälle wir leicht lösen können.
1-stellig 1-ziffrig ist einfach, da gibt es genau die 10 Zahlen 0, 1, 2, …, 9
2-stellig 1-ziffrig geht auch nur 10x, 00, 11, 22, … 99 und das gilt für eine beliebige Zahl von Stellen. Es gibt für jedes $n$ 10 $n$-stellig 1-ziffrige Zahlen; wir können ja jede $n-1$-stellige 1-ziffrige Zahl nur unter Verwendung der einen bereits verwendeten Ziffer zu einer $n$-stelligen 1-ziffrigen Zahl verlängern. Wir wissen also jetzt, dass es 10 2-stellige 1-ziffrige Zahlen gibt. Da es insgesamt 100 2-stellige Zahlen gibt, gibt es 90 2-stellig 2-ziffrige Zahlen. Wir können die Anzahl der Zahlen mit lauter verschiedenen Ziffern für jede beliebige Stellenzahl ausrechnen. Für die erste Stelle gibt es 10 Möglichkeiten, jede dieser 1-stelligen Zahlen kann auf 9 Arten zu einer 2-stellig 2-ziffrigen Zahl verlängert werden.
Jede dieser 90 2-stellig 2-ziffrigen Zahlen kann auf 8 Arten zu einer 3-stellig 3-ziffrigen Zahl verlängert werden, also gibt es $10\cdot 9\cdot 8=720$ 3-stellig 3-ziffrige Zahlen.
4-stellig 4-ziffrige Zahlen gibt es daher $10\cdot 9\cdot 8\cdot 7=5040$, und dieses Rechenrezept können wir bis zu 10-stelligen Zahlen verwenden. 11-stellige Zahlen mit lauter verschiedenen Ziffern kann es ja nicht geben, wenn nur 10 Ziffern zur Verfügung stehen. Das gilt auch für viele anderer Fälle: Es gibt keine Zahlen, die mehr verschiedene Ziffern verwenden als sie Stellen haben. Wir wissen jetzt, dass 10 3-stellig 1-ziffrige und 720 3-stellig 3-ziffrige Zahlen gibt. Daher gibt es $1000-10-720=270$ 3-stellig 2-ziffrige Zahlen.
Wir können das, was wir uns bisher überlegt haben, in einer Tabelle zusammenfassen:
Jetzt stellen wir eine neue Reihe mit 6 Schachteln (wieder nummeriert von 1 bis 6) auf. Dann erzeugen wir von jedem Zettel in Schachtel 1 (aus der Reihe für die 3-stelligen Zahlen) 10 Kopien und hängen an die 3-stellige Zahl jeweils eine der 10 Ziffern an. So entstehen 4-stellige Zahlen. Diese Zahlen legen wir in die „richtigen“ Schachteln für die 4-stelligen Zahlen. Wenn wir die 2-stellig 1-ziffrigen Zahlen mit jeweils einer Ziffer verlängern (z.B. 111), dann bekommen wir 1 4-stellig 1-ziffrige Zahl (nämlich 1111) und 9 4-stellig 2-ziffrige Zahlen (1111, 1112, 1113, …, 1119, 1110). Eine unserer verlängerten Zahlen hat also die gleich „Ziffrigkeit“ und bei 9 verlängerten Zahlen wird die Ziffrigkeit um 1 höher.
Wenn wir 3-stellig 2-ziffrige Zahlen (z.B. 121) mit allen 10 möglichen Ziffern verlängern, dann sind 2 der Verlängerungen wieder 2-ziffrig (1211 und 1212) und die übrigen 8 Verlängerungen sind 3-ziffrig. Wir haben also aus den 10 3-stellig 1-ziffrigen Zahlen 90 4-stellig 2-ziffrige Zahlen erzeugt, und aus den 270 3-stellig 2-ziffrigen ebenfalls $2\cdot 270=540$ 4-stellig 2-ziffrige Zahlen, insgesamt also $9\cdot 10+2\cdot 270=630$ 4-stellig 2-ziffrige Zahlen. Es gibt ja keine andere Art, solche Zahlen durch Verlängerung 3-stelliger Zahlen zu erzeugen, daher sind das alle derartigen Zahlen. Mit den gleichen Überlegungen können wir sehen, dass wir alle 4-stellig 3-ziffrigen Zahlen aus den 3-stellig 2-ziffrigen und den 3-stellig 3-ziffrigen erzeugen können. Jede 3-stellig 2-ziffrige Zahl kann auf 8 Arten zu einer 4-stellig 3-ziffrigen verlängert werden (wir hängen einfach hinten eine der 8 noch nicht verwendeten Ziffern an), und jede 3-stellig 3-ziffrige Zahl kann auf 3 Arten zu einer 4-stellig 3-ziffrigen Zahl verlängert werden, indem wir jeweils eine der 3 schon verwendeten Ziffern hinten anhängen.
Es gibt daher $8\cdot 270+3\cdot 720=3600$ 4-stellig 3-ziffrige Zahlen.
Das Rezept funktioniert auch für die 4-stellig 4-ziffrigen Zahlen: Jede 3-stellig 3-ziffrige Zahl kann auf 7 Arten (mit einer der $10-3$ noch nicht verwendeten Ziffern) zu einer 4-stellig 4-ziffrigen Zahl erweitert werden. 3-stellig 4-ziffrige Zahlen gibt es nicht, daher ist der zweite Ausdruck in der Summe, die wir typischerweise berechnen, einfach 0. In unserer Tabelle können wir das Muster unserer Rechnung so beschreiben: in jeder Zelle steht eine Summe aus 2 Produkten. Das erste Produkt ist die Zahl links darüber multipliziert mit (10-Spaltennummer) der Spalte, aus der diese Zahl kommt, das zweite Produkt ist die Zahl unmittelbar darüber multipliziert mit der Spaltennummer dieser Spalte.
Diese Rechnung gilt für alle 2- oder mehrstelligen und 2- oder mehrziffrigen Zahlen. Die so vervollständigte Tabelle sieht so aus:
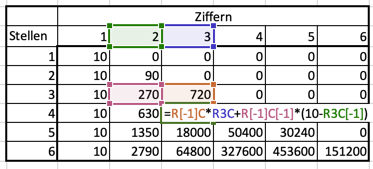
rosa . grün + orange . blau. Die Formelschreibweise ist vielleicht nicht die, die sie normalerweise in Excel sehen. Man kann sie aber in den Excel-Optionen einschalten. R[-1]C bedeutet beispielsweise Zeile (englisch row) darüber, selbe Spalte (englisch column). Wenn ihr Excel auf deutsch eingestellt ist, dann steht dort Z[-1]SZ3S+Z[-1]S[-1]Z3S[-1] Wir sehen in dieser Tabelle, dass es 327600 6-stellige 4-ziffrige Zahlen gibt. Übersetzt in die „übliche“ mathematische Schreibweise lautet die Lösung unseres Problem so: $$F(1,1)=10\\
F(n,1)=10 \text{ für } n>1 \\
F(1,k) = 0 \text{ für } k>1 \\
F(n,k) = (10-(k-1))F(n-1,k-1)+k F(n-1,k)\text{ sonst}
$$ $F(n,k)$ ist dabei die Zahl in der Zelle mit Zeilennummer $n$ und Spaltennummer $k$. Die Formel ist also inhaltlich vollkommen gleich mit der verbalen Beschreibung der Tabelle; sie drückt das Rechenrezept nur in der in der Mathematik üblichen sehr kompakten Schreibweise aus. Zusatzanmerkung:
Wir haben die Anzahl der Zahlen mit lauter verschiedenen Ziffern als $10$, $10 \cdot 9$, $10 \cdot 9 \cdot 8$ usw. berechnet. Diese Zahlen sind strukturell Potenzen ähnlich. $n^k$ bedeutet, dass man die Zahl $n$ $k$-mal mit sich selbst multipliziert, wir berechnen also
$$
\underbrace{n . n \ldots n }_\text{k Faktoren}
$$ Die Produkte, die wir berechnen, haben auch k Faktoren, allerdings ist jeder davon um 1 weniger als der vorhergehende: $$
\underbrace{n . (n-1).(n-2) \ldots (n-k+1) }_\text{k Faktoren}
$$ Diese Produkte haben einen eigenen Namen, sie heißen fallende Faktorielle, oder fallende faktorielle Potenzen. Sie kommen in der Kombinatorik so oft vor, dass es eigene Schreibweisen dafür gibt, nämlich $$ n^\underline{k} \text{ oder } n_{(k)}$$ Die mathematische Definition lautet $$ n^\underline{k} = \prod_{i=0}^{k-1}(n-i)$$ Falls sie diese mathematische Schreibweise nicht gewohnt sind, sollten sie sich davon nicht schrecken lassen. Sie bedeutet nichts anderes als das, was wir schon in Worten ausgedrückt haben. Die oben stehende unterstrichene Zahl (der Exponent) gibt an, wieviele Faktoren das Produkt hat und die unten stehende Zahl ist der erste Faktor; alle weiteren Faktoren werden pro Faktor um 1 verringert.