Nochmals statistische Nachlese zur Bundespräsidenten-Wahlaufhebung
Ich habe meine statistischen Überlegungen zur Aufhebung des 2. Wahlgangs der Bundespräsidentenwahl jetzt in einem interaktiven Dokument
aufbereitet.
Gerhart-Bruckmann-Preis
Ich habe – worüber ich mich sehr freue – den Gerhart-Bruckmann-Preis 2017 „für Aktivitäten, die dazu beigetragen haben, den Stellenwert der Statistik in der Öffentlichkeit zu verbessern“ verliehen bekommen.
Hier das Link zu meinen Festvortrag und den Details zu diesem Preis
Ein kurzes Video (© Martin Troger) vom Ende der Laudatio, die Gerhart Bruckmann gehalten hat, gibts auch.
Brauchen wir spezielle Taschenrechner im Mathematik-Unterricht?
Vor einigen Tagen war ich auf Twitter eine Diskussion zum Thema „Schultaschenrechner” verwickelt.
Ausgangspunkt war ein Artikel auf heise.de
Dieses Thema hat zwei Aspekte; als erstes den, der in dem Artikel angesprochen wird:
Sind diese Rechner durch das Duopol der Hersteller nicht eigentlich viel zu teuer?
Das wichtigere Thema ist allerdings: ist diese Art von Taschenrechner überhaupt ein sinnvolles und zeitgemäßes Hilfsmittel?
Die anspruchsvollen Taschenrechner vom Casio und Texas Instruments,
die in der Sekundarstufe II verwendet werden, decken normalerweise
drei mathematische Teilbereiche ab:
- Numerisches Rechnen, mit Winkel-, Exponential- und Logarithmusfunktionen
- Funktionsschaubilder
- algebraisches Rechnen (Termumformungen, Lösen von Gleichungen)
Auf den besonders gut ausgestatteten Geräten gibt es dann auch noch
Module zu dynamischer Geometrie.
Mit diesen Geräten gibt es aus didaktischer Sicht ein fundamentales Problem:
Außerhalb des Schulunterrichts werden sie praktisch nirgends verwendet.
Die Schule vermittelt also im Mathematikunterricht als eine der zentralen Botschaften: In Mathematik in der Schule verwenden wir Werkzeuge, die kein Mensch außerhalb der Schule je verwendet.
Dabei gibt es dieselben mathematischen Werkzeuge auch auf Geräten, die die meisten Schüler(innen)? schon haben: Smartphones und Tablets.
Für diese Geräte gibt sehr viele Apps, die all das abdecken, was die Taschenrechner können.
Da fast alle diese Geräte auch schon eine Kamera eingebaut haben können sie sogar noch mehr:
Photomath und Mathpix können mathematische Ausdrücke abfotografieren, erkennen und dann weiterbearbeiten. Man kann also eine eine gedruckte Gleichung oder sogar eine
auf Papier mit der Hand geschriebene Gleichung abfotografieren und dann von der App lösen lassen. Wenn man will kann man sich den Lösungsweg sogar Schritt für Schritt vorführen lassen.
Für dynamische Geometrie gibt es GeoGebra.
Es gibt also Geräte, die die meisten Schüler(innen)? schon selber haben, die man direkt im Mathematikunterricht einsetzen könnte. Die jungen Leute würden also sehen, dass Geräte, die in ihrem Alltag außerhalb der Schule eine wesentliche Rolle spielen, auch im Mathematikunterricht eine entscheidendene Hilfe sein können.
In vielen Schulen ist allerdings der Gebrauch vom Handys während der Unterrichtszeit strikt verboten. Statt Mühe darauf zu verwenden, schulisches und außerschulisches Leben miteinander zu verbinden, sperrt die Schule außerschulisches Leben aus!
Ein möglicherweise vorgebrachtes Argument, nämlich dass es sich bei den Smartphones und Tablets der Schüler(innen)? um Produkte verschiedener Herstellen handelt und daher nicht alle dieselben Werkzeuge zur Verfügung hätten beruht auf einem Missverständnis. Das mathematische Werkzeug ist das Programm, nicht der Rechner oder das Smartphone, und die angeführten Apps gibt es sowohl für Android als auch für iOS, also für praktisch alle gängigen Smartphones und Tablets.
Beim Rechnereinsatz im Mathematik-Unterricht sollte man aber vor allem Folgendes bedenken: Im Leben außerhalb der Schule wird der überwältigende Anteil aller Aufgaben, bei denen gerechnet werden muss, mit Excel (von Microsoft) gerechnet. Das ist DAS Standard-Werkzeug für numerisches Rechnen. Das wirkt sich auf den Mathematikunterricht bisher nur in sehr geringem Umfang aus. Excel deckt die Bereiche numerisches Rechnen und Funktionsschaubilder vollständig ab, und es bietet einige zusätzliche Möglichkeiten.
Und es ist sowohl für Android als auch für iOS verfügbar, passt also eine Smartphone/Tablet-Strategie.
Es gibt heute wirklich keinen ernstzunehmenden Grund mehr, spezielle Taschenrechner für den Mathematikunterricht anzuschaffen.
P.S.: Vielleicht haben sie sich gewundert, warum da Schüler(innen)? steht.
Das ist der Mechanismus, den ich fürs gendersensible Schreiben verwende. Er kommt aus der Informatik und heißt „reguläre Ausdrücke”. Wenn eine Buchstabenfolge in Klammern steht und unmittelbar danach ein Fragezeichen, dann bedeutet das, dass diese Buchstabenfolge an dieser Stelle einmal (nicht öfter) oder eben nicht vorkommen kann. Ein geklammerter Ausdruck mit gleich danach einem Plus-Zeichen heißt, dass dieser Ausdruck mindesten einmal, aber auch öfter, nämlich beliebig oft vorkommen kann.
(ha)+ kann also ha, haha, hahaha, hahahaha … sein.
Ein geklammerter Ausdruck mit mehreren senkrechten Strichen bedeutet, dass genau einer der Teilausdrücke verwendet werden kann.
(jetzt|immer|nie) kann also jetzt oder immer oder nie sein.
PISA in Österreich – Geschlecht und Schultyp
Im falter 5/17 ist ein Artikel von mir zum Thema PISA erschienen. Der Artikel ist allerdings nicht gratis zu lesen.
In diesem Artikel wird auch auf erweiterte Analysen und die notwendigen Daten in diesem Blog verwiesen.
Einen Teil der erweiterten Analyse (sämtliche PISA Ergebnisse aus allen EU-Staaten) gibts in einem früheren Blogbeitrag.
Hier noch die zusätzliche erweiterte Analysen, nämlich sämtlich PISA-Ergebnisse aus Lesen, Mathematik und Naturwissenschaften aus Österreich, gegliedert nach Schultyp.
Die Ergebnisse für 2009 sind laut OECD mit großer Vorsicht zu interpretieren, durch eine Boykottaufruf wurde ein Teil der Ergebnisse
höchstwahrscheinlich verfälscht.
Die letzte dieser Tabellen gibt die Anteile der Schüler in den einzelnen Schultypen an (Sonderschüler und Schüler mit unbekanntem Schultyp wurden vor den Berechnungen aus den Daten ausgeschieden).
Interessant ist auch die Analyse getrennt nach Geschlechtern:
Die beiden Anteilstabellen am Schluss geben einmal die Anteile derr Schultypen berechnet an Mädchen und Burschen getrennt und einmal berechnet an allen Schülern und Schülerinnen gemeinsam an.
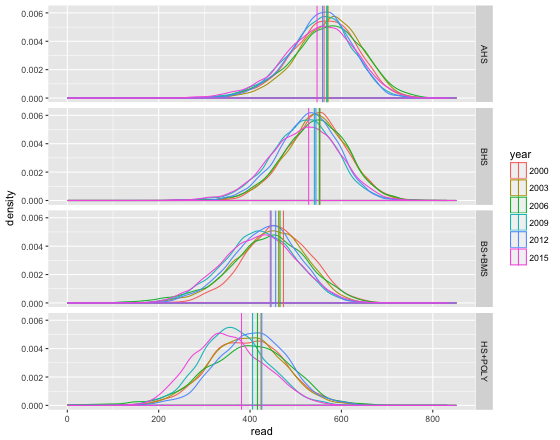
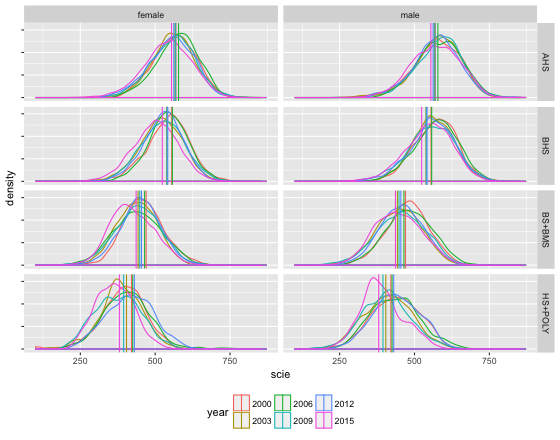
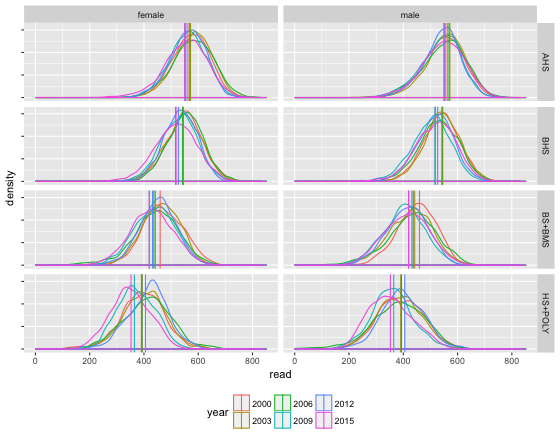
Unterschiede zwischen den Verteilungen der Werte erkennt man einfacher mit grafischen Darstellungen, nämlich mit Dichteschaubildern. Die Kurven geben an, in in welchen Bereichen der PISA-Scores es mehr und in welchen Bereichen es weniger Schüler gibt.
Die senkrechten Linien markieren die Mittelwerte aus den eben engeführten Tabellen.
Fürs Lesen schaut das getrennt nach Schultypen so aus:
Man sieht ganz deutlich, dass es zwischen den einzelne Schultypen große Leistungsunterschiede gibt.
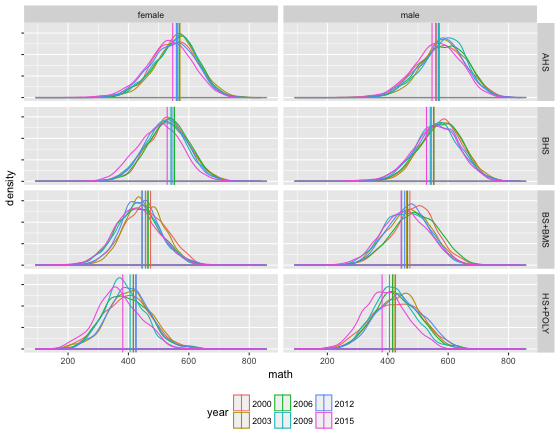
nach Geschlechter getrennt schauen die Verteilungen so aus.
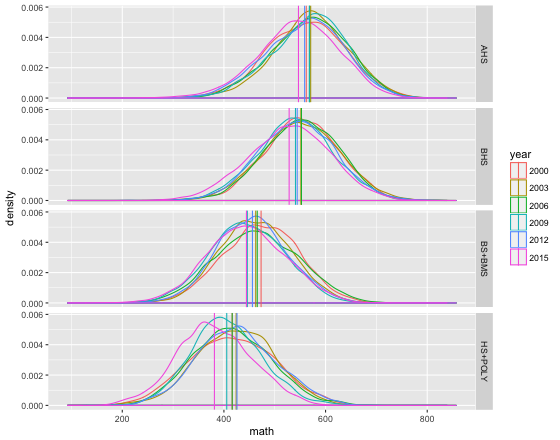
Für Mathematik ergibt sich folgendes Bild
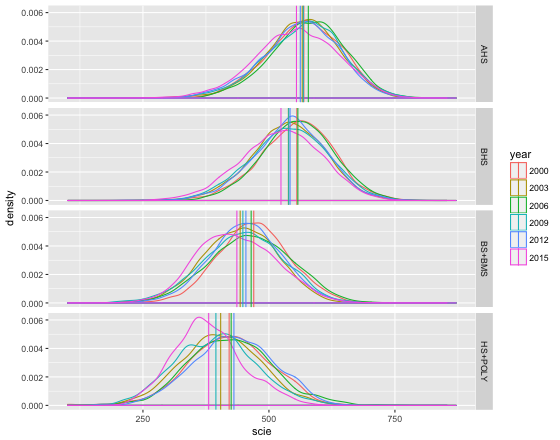
Für die Naturwissenschaften schein die Verteilungen so aus:
Die Daten für diese Analyse können sie als Excel-Arbeitsmappe herunterladen.
Sind die PISA-Ergebnisse 2012 und 2015 vergleichbar?
In der Diskussion um die PISA-Ergebnisse wird sehr wenig darüber gesprochen, dass bei Abwicklung des Tests eine ziemlich bedeutsame Änderung vorgenommen wurde: 2012 mussten die getesteten Jugendlichen noch mit Arbeitsblättern aus Papier arbeiten, 2015 wurde der Test auf Computern abgewickelt.
Eine derartig radikale Umstellung des Testverfahrens kann natürlich auf die Ergebnisse einen starken Einfluss haben.
Wir sehen uns daher die Testergebnisse in Hinblick auf möglicherweise dadurch verursachte Veränderungen genauer an.
An PISA nehmen so verschiedene Länder wie Österreich, Indien, Japan und Mexiko teil. Da ist zu erwarten, dass es abgesehen von der Abwicklung des Tests noch weitere sehr große für PISA relevante Unterschiede gibt. Beschränken wir uns beim Vergleich auf die EU-Staaten. Es gibt derzeit 27 EU-Länder. Mit Ausnahme von Malta haben alle an PISA 2012 und PISA 2015 teilgenommen, wir untersuchen also 26 Länder.
Sehen wir uns die Lese-Ergebnisse in diese Ländern (gegliedert nach Geschlecht) an.
Lese-Ergebnisse PISA 2012 und 2015 – EU-Staaten
Die drittletzte und die vorletzte Spalte zeigen die Geschlechterdifferenz beim Lesen für alle 26 Länder.
In allen untersuchten Ländern schneiden die Mädchen in beiden Testperioden beim Lesen deutlich besser ab als die Buben, und die entsprechenden Punktedifferenzen sind teilweise dramatisch hoch (über 50 Punkte).
Die letzte Spalte der Tabelle gibt an, wie sich der Geschlechterunterschied im Lesen von 2012 auf 2015 verändert hat, und da stellen wir fest, dass er in *allen* Ländern kleiner geworden ist, in 13 der 26 Länder um 15 oder mehr Punkte.
In 15 der 26 Länder haben sich die Mädchen verschlechtert und die Buben verbessert.
In 3 Ländern (Slowenien, Spanien und Schweden) haben sich die Mädchen zwar im Lesen verbessert, die Buben deutlich stärker; da die Buben überall im Lesen schlechter als die Mädchen sind, hat sich daher in diesen Ländern die Geschlechterdifferenz verringert.
In 7 der 26 Länder (Belgien, Griechenland, Ungarn, Luxemburg, Niederlande, Polen und Slowakei) haben sich Buben und Mädchen verschlechtert, die Verschlechterung bei den Buben war aber kleiner als die bei den Mädchen, also hat auch in diesen Ländern die Geschlechterdifferenz abgenommen.
Man kann wohl nicht davon ausgehen, dass die Verringerung der Geschlechterdifferenz im Lesen darauf zurückzuführen ist, dass alle diese 26 Länder gleichzeitig bildungspolitische Maßnahmen zur Verringerung dieser Geschlechterdifferenz wirksam umsetzen konnten.
Eine deutlich plausiblere Erklärung erscheint da, dass sich die Umstellung von papierbasiertem auf computerbasiertes Testverfahren bei den Mädchen anders ausgewirkt hat als bei den Buben.
Wenn das der Fall ist, dann bedeutet das, dass man bei Vergleichen von früheren mit den aktuellen PISA-Ergebnissen mit höchster Vorsicht umgehen muss.
Wenn man ein Messverfahren ändert, dann kann man die gemessenen Werte nicht mehr ohne zusätzliche Analyse vergleichen.
Die folgenden Tabellen zeigen, dass die Änderung der Testabwicklung in Mathematik und den Naturwissenschaften nicht so über die Länder hinweg homogene Auswirkungen auf die Geschlechterdifferenzen hatte.