Wie breiten sich Epidemien aus?

Es gibt sehr viele Informationen zur Entwicklung der Zahl der COVID-19 Erkrankten.

Unter anderem heißt es, dass es wichtig ist, die Kurve zu verflachen.

Ich habe ein kleines mathematisches Modell erstellt, der das entsprechende Phänomen illustriert.

In diesem Modell gibt es drei Gruppen in der Gesamtpopulation:

• Suszeptible (Noch nicht erkrankte, die noch erkranken können)
• Infizierte
• Gesundete

Das Modell geht grob vereinfachend davon aus, dass einmal Gesundete nicht mehr erkranken und auch keine anderen mehr infizieren können (Todesfälle berücksichtigt das Modell nicht).

Die Fortschreibung der Zahlen im Modell funktioniert so.
Wir gehen davon aus, dass jede Person pro Tag eine fixe Zahl von Kontakten mit anderen Personen hat. Bei einem Kontakt zwischen einer suzeptiblen und einer infizierten Person kommt es mit einer bestimmten Wahrscheinlichkeit zu einer Infektion; in diesem Fall wird die suszeptible Person zur infizierten Person.
Eine weitere Modellannahme besagt, dass jede infizierte Person nach einem fixen Zeitraum gesund wird.

Die Mathematik dahinter funktioniert so:
Wenn der Anteil der Infizierten in der Bevölkerung $p_I$ ist und jede Person z.B. 10 Kontakte hat,
dann kann eine suszeptible Person 0, 1, 2 bis 10 Kontakte mit Infizierten haben. Die Wahrscheinlichkeit für jeden dieser Fälle kann man (mit einer Binomialverteilung als ) ausrechnen.
Die Wahrscheinlichkeit, dass es bei insgesamt 10 Kontakten zu 3 Kontakten mit Infizierten kommt, ist dann $\binom{10}{3}p_I^3(1-p_I)^7$.
Wenn ein Suszeptibler 3 Kontakte mit Infizierten hat, dann kann man die Wahrscheinlichkeit dafür, dass er infiziert wird berechenen. Diese Wahrscheinlichkeit ist dann $1-(1-p_A)^3$. Diese beiden Überlegungen kombiniert man und berechnet damit die Wahrscheinlichkeit, dass ein Suszeptibler beim aktuellen Infiziertenanteil infiziert wird.

Wenn also jede Person $n$ Kontakte (pro Tag) hat, $p_I$ der Anteil der Infizierten und $p_A$ die Ansteckungswahrscheinlichkeit bei einem Konrakt zwischen Suszeptiblem und Infiziertem ist,
dann ist die durchschnittliche Ansteckungswahrscheinlichkeit für Suszeptible in der Population

$$\bar{p}=\sum_{i=0}^{n}\binom{n}{i}p_I^i (1-p_I)^{n-i}(1-(1-p_A)^i)$$

Wenn es an einem Tag $t$ $S(t)$ Suzeptible gibt, dann werden an diesem Tag $N(t)=S(t)\bar{p}$ davon neu infiziert, die Zahl der Suszeptiblen wird also um diese Zahl weniger und beträgt am nächsten Tag $S(t+1)=S(t)-N(t)$.

Die Zahl der Infizierten $I(t)$ erhöht sich um die neu Infizierten $N(t)$.
Andererseits werden auch Infizierte wieder gesund, und zwar alle, die vor $d$ ($d$ steht für Dauer der Erkrankung) Tagen neu infiziert wurden, also um $N(t-d)$. In den ersten $d$ Tagen nach Beginn der Epidemie ist die Zahl der Gesundeten natürlich noch 0, es ist ja noch niemand lang genug krank, um schon wieder gesund zu werden. Daher ist die Zahl der Infizierten am Tag $t+1$ $I(t+1)=I(t)+N(t)-N(t-d)$.

Die Gesamtzahl der Gesundeten ist am Tag $t+1$, $G(t+1)$, ist die Zahl der Gesundeten von Vortag plus der Zahl der neu Gesundeten, also die Zahl der von $d$ Tagen neu Infizierten,
$G(t+1)=G(t)+N(t-d)$.

Dieses Modell gibt es als Spreadsheet zum herunterlanden.

Achtung: das Spreadsheet enthält Makros, es funktioniert nur, wenn die Ausführung von Makros erlaubt ist.

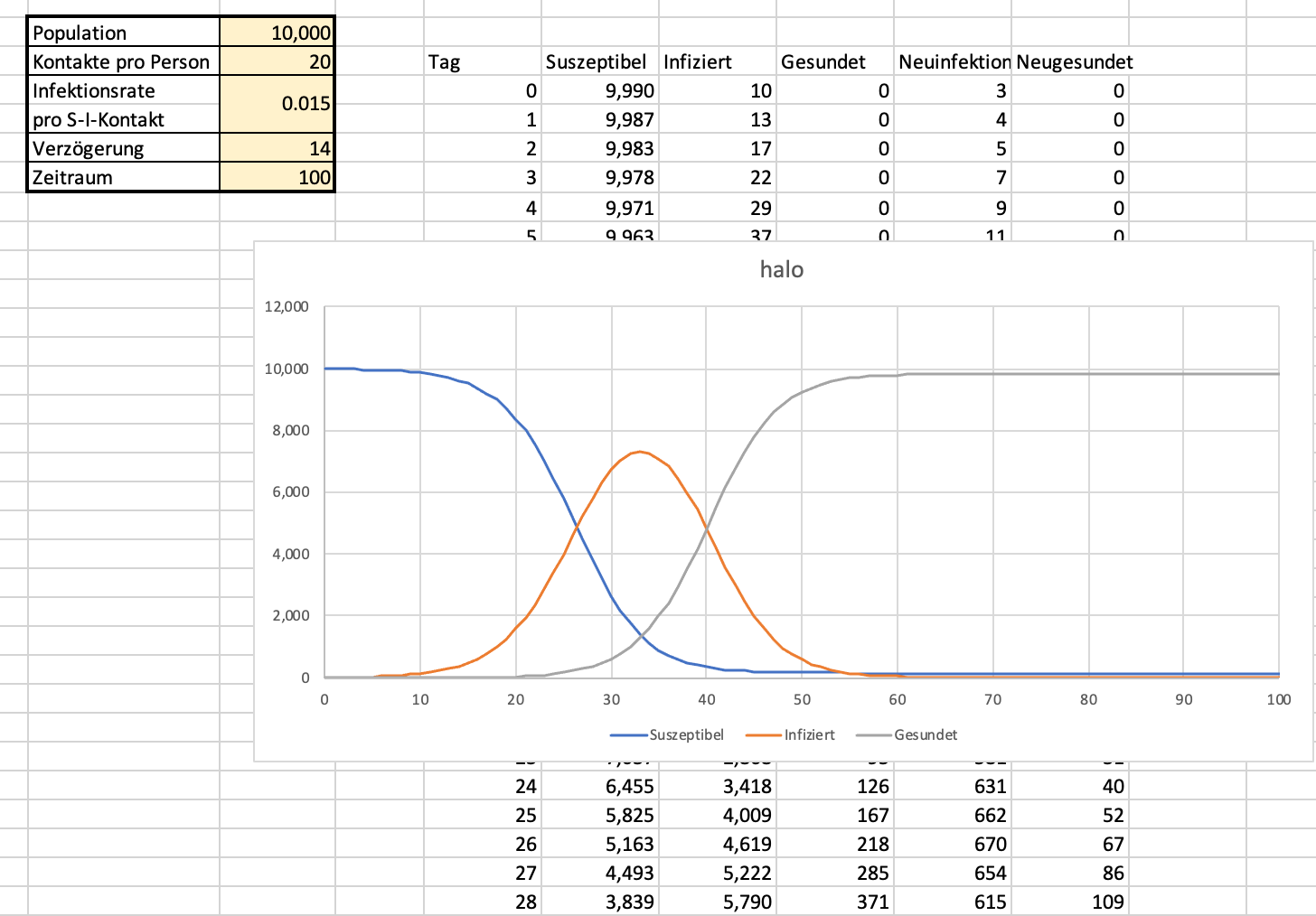
Sie können die Werte in den farbig unterlegten Zellen ändern und sehen, wie sich das auf die Verlaufskurve der Infizierten auswirkt.

Insbesondere können sie sehen, dass die Verringerung der Kontakte die Kurve der Infizierten verflacht und nach rechts verschiebt.

Das Modell geht davon aus, dass jede Person mit jeder andern mit gleicher Wahrscheinlichkeit in Kontakt kommt. Das ist natürlich für ganz Österreich (mit 9 Millionen Einwohnern) nicht realistisch. Daher geht dieses Modell zunächst von einer Bevölkerung von 10.000 aus. Das entspricht einer mittelgroßen Stadt in Österreich.

Alle markierten Werte können aber einfach geändert werden. Wenn die Bevölkerung größer ist, dann ist der gesamte Verlauf (in diesem Modell) etwas langsamer. Deshalb kann mit dem Wert Zeitraum eingestellt werden, über wieviele Tage sich die Kurve erstrecken soll.

Das Modell ist natürlich sehr vereinfachend. Dazu passt ein Aphorismus vom George Box, einem berühmten Statistiker:

Alle models are wrong, but some models are useful.

Ich hoffe, dass mein Modell für die Leser zur nützlichen Kategorie zählt.