Magische Quadrate: was geht und was geht nicht

Vor ein paar Tagen meldete sich ein besorgter Elternteil eines Volksschulkindes auf Twitter mit der Bitte um Hilfe bei einem Problem aus dem Mathematikbuch des Kindes.

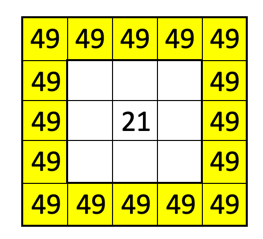
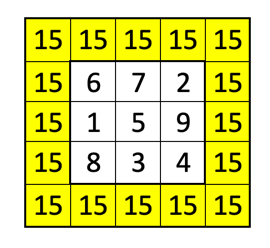
Die Seite mit den Aufgaben sah etwa so aus:

Und noch etwas für Rechenmeister!

Es geht bei den Aufgaben natürlich darum, die leeren Kästchen so mit Zahlen zu füllen, dass alle Zeilensummen, alle Spaltensummen und die Summen über beide Diagonalen gleich sind.

Die Aufgabe links oben hatte das Kind gelöst. Bei der Aufgabe rechts oben gabs einen (leider nicht richtigen) Lösungsversuch. Bei der Aufgabe links unten fand das Kind keine Lösung, und die Eltern auch nicht. Deshalb der Hilferuf auf Twitter.

Das ist nicht weiter verwunderlich, denn die Aufgabe ist (so wie die Aufgabe rechts oben) nicht lösbar!

Wie kann man das zeigen?

Gehen wir es als Mathematiker gleich allgemeiner an, statt der gegebenen Aufgabe

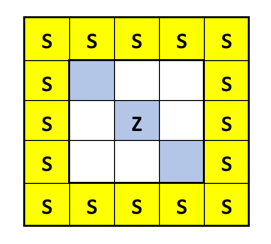
untersuchen wir Aufgaben, wo alle Summen und die Zahl in der Mitte vorgegeben sind, ohne diese Zahlen schon festzulegen:

Wir bilden jetzt eine Summe aus Zeilen, Spalten und Diagonalen und beginnen mit der Diagonale von links oben nach rechts unten:

Die Summe der blau markierten Felder ist natürlich s.

Jetzt addieren wir die andere Diagonale:

Die Summe ist 2﹒s, und in der Summe der beiden Diagonalen steckt s 2x drinnen.

Jetzt addieren wir noch die mittlere Spalte:

Diese Summe (Beide Diagonalen + mittlere Spalte) ist 3﹒s und die Zahl z in der Mitte steckt 3x in Dieser Summe drinnen.

Jetzt ziehen wir die erste und die dritte Zeile ab:

Dann bleibt von unserer ganzen Summe:
Diagonale links oben → rechts unten +
Diagonale rechts oben → links unten +
mittlere Spalte –
erste Zeile –
dritte Zeile

Nur die Zahl in der Mitte über, und sie kommt 3x vor.

Also gibts bei solchen Aufgaben nur dann eine Lösung, wenn alle Summen das Dreifache der Zahl in der Mitte sind.

Das ist bei der Aufgabe im Schulbuch nicht der Fall, daher kann man die Aufgabe nicht lösen.

Wir können aber aus dem, was wir uns gerade überlegt haben, noch mehr folgern.

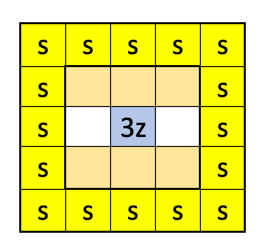
Nehmen wir die mittlere Zeile her:

Wir wissen schon, dass die Zeilensumme das dreifache der mittleren Zahl sein muss.

Wenn da beispielsweise im orangen Kästchen z-2 steht, dann muss im grünen Kästchen z+2 stehen (nur so erhalten wir die Summe 3z)

Zu dieser Zeile gehört also eine „Abweichung“, das ist eine Zahl, die auf der einen Seite zu z addiert und auf der anderen Seite von z abgezogen wird.
Genauso muss es für die mittlere Spalte und für die beiden Diagonalen Abweichungszahlen geben.

Ein besonderer Fall ist der, wo alle Summen 0 sein sollen und daher auch 0 im mittleren Kästchen steht,

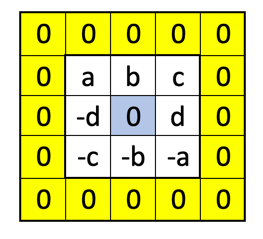
Nennen wir die 4 Abweichungszahlen a, b, c und d,
dann haben wir folgendes Quadrat:

Damit auch die oberste Zeile die vorgegebene Summe 0 hat muss a+b+c=0 sein und damit die linke Spalte Summe 0 hat muss a-d-c=0 sein.

Das geht zum Beispiel so:

Durch Drehen um 90º, 180º und 270º kann man 3 weitere Lösungen draus machen, und durch Spiegeln um die waagrechte und senkrechte Mitte sowie um die beiden Diagonalen kann man 4 weitere Lösungen draus machen. Wenn als Abstandszahlen nur 1, 2, 3 und 4 erlaubt sind, dann sind das alle Lösungen, die es gibt (das kann man durch Ausprobieren nachprüfen).

Wenn man zu allen Zahlen dieses Quadrats dieselbe Zahl addiert, dann sind wieder alle Summen gleich (zu allen Summen kommt 3x die addierte Zahl dazu), und so kann man alle Quadrate mit der Summeneigenschaft erhalten. Da alle Summen um das dreifache einer Zahl größer werden gibts derartige Zahlenquadrate nur für durch 3 teilbare Summen.

Wenn wir in das mittlere Kästchen 5 schreiben und die Tabelle mit denselben Abstandszahlen bilden, dann erhalten wir:

Dieses Quadrat hat eine besondere Eigenschaft, es kommen alle Zahlen von 1 bis 9 genau einmal vor.

Solche Quadrate nennt man Magische Quadrate, und in der Wikipedia findet man dazu mehr Informationen.

P.S.: Die Aufgabe rechts oben ist nicht (mit ganzen Zahlen) lösbar, weil ein Drittel von 23 keine ganze Zahl ist.