7-fach-Jackpot im Lotto: Wie wahrscheinlich ist so etwas?

Wir haben das erste Mal seit es das Lotto 6 aus 45 gibt, also seit September 1986, einen 7-fachen Jackpot.

Es gab bisher 2784 Spielrunden.

Man kann fragen, wie groß die Wahrscheinlichkeit ist, dass bei so vielen Lottorunden 7x hintereinander keine Spieler die 6 Richtigen tippt.

Es gibt allerdings keine einfache Antwort auf diese Frage.

Um die Wahrscheinlichkeit eines Jackpots auszurechnen braucht eine Annahme und eine Zahl.

Die Annahme lautet, dass die Spieler alle möglichen Tipps mit gleicher Wahrscheinlichkeit setzen. Das ist aber nicht der Fall, weil Zahlen über 31 seltener gesetzt werden, weil diese Zahlen keinem Datum (z.B. einem Geburtstag) entsprechen.

Die Zahl, die wir brauchen, ist die Zahl der in eine Runde abgegebenen Tipps. Diese Zahl schwankt bei 6 aus 45.

Wäre die Zahl der abgegebenen Tipps pro Runde für alle Runden gleich, dann könnte man die Wahrscheinlichkeit für einzelne Jackpotrunde einfach ausrechnen.

Die Zahl der Tipps pro Runde schwankt aber seit Bestehen des Lottos, und zwar zwischen 2.6 Millionen und 52 Millionen, also ganz beträchtlich.

Bei Einführung von 6 aus 45 gab es nur eine Ziehung pro Woche, und zwar am Sonntag. Seit September 1997 gibt es jede Woche 2 Ziehungen pro Woche, am Sonntag und am Mittwoch. Im Schnitt wurden in den Sonntagsziehungen bis September 1997 jeweils 16 Millionen Tipps abgegeben, danach in Mittwochrunden 6 und in Sonntagsrunden 7 Millionen Tipps.

Typischerweise werden in Jackpotrunden mehr Tipps als in „normalen“ Runden abgegeben. Allerdings sind die entsprechenden Zahlen für die alten und die neuen Sonntagsziehungen und die Mittwochsziehungen merkbar verschieden. Bis September 1997 wurden in Normalrunden im Schnitt 14.3 und in Jackpotrunden 21.8 Tipps abgegeben. Bei den Sonntagsrunden nach September 1997 wurden in Normalrunden 5.9 und in Jackpotrunden 8.4 Millionen Tipps angegeben, in Mittwochrunden 4.5 bzw. 7.7 Millionen Tipps.

Wir können die Wahrscheinlichekt für 7 oder mehr Jackpots hintereinander genaugenommen nur berechnen, wenn die Zahl der Tipps pro Runde gleich ist. Das ist bei uns nicht der Fall. Seit September 1997 wurden durchschnittlich 6.6 Millionen Tipps pro Runde abgegeben.
Wenn wir mit dieser Zahl von Tipps die Wahrscheinlichkeit für einen Jackpot errechnen, dann bekommen wir

$$
\left(1-\frac{1}{\binom{45}{6}}\right)^{6600000}=\left(1-\frac{1}{8145060}\right)^{6600000}=0.450
$$

Rechnen wir mit dieser Jackpotwahrscheinlichkeit pro Runde die Wahrscheinlichkeit für mindestens 7 Jackpots in Folge in 2211 Runden aus, dann erhalten wir dafür eine Wahrscheinlichkeit von 0.99994

Wenn 7 Jackpots in Folge so wahrscheinlich sind, warum ist das dann bisher noch nicht vorgekommen?

Der Hauptgrund ist wohl, dass die Tippzahl pro Runden nicht gleich ist sondern bei Mehrfachjackpots steigt.

In den letzten 7 (6erfreien) Runden wurden 3.0, 3.8, 4.4, 5.1, 6.8, 8.3 und 12.3 Millionen Tipps abgegeben.

Die Wahrscheinlichkeit für einen Jackpot hängt von der Tippzahl ab und nimmt mit höherer Tippzahl ab. Je mehr Jackpots es also direkt vor eine Runde gab, desto geringer ist die Wahrscheinlichkeit, dass es in der neuen Runde zu einem Jackpot kommt.

Es gibt in der Wahrscheinlichkeitsrechnung einfach formulierbare Aufgaben, die man nicht so einfach ausrechnen kann. Die Frage nach der Wahrscheinlichkeit für einen 7fach-Jackpot ist so eine Frage.

P.S.: Die Formel für die Berechnung der Wahrscheinlichkeit für mindestes 7 Jackpots hintereinander finden sie hier nicht, weil sie relativ kompliziert ist und tiefergehendes Verständnis für Berechnung mit rekursiv definierten Funktionen erfordert.

Für absolute Mathenerds:

Die Berechnung der Wahrscheinlichkeit $P(n,k,p)$, dass in einer Folge von $n$ Versuchen höchstens $k$ Ereignisse mit einer Einzelwahrscheinlichkeit $p$ unmittelbar aufeinander folgen, geht mit folgender Formel:

$$
P(n,k,p)=\begin{cases}1 & \text{für }n \leq k \\
1-p^{k+1} & \text{für }n = k+1 \\
\sum_{i=1}^{k+1}P(n-i,k,p)p^{i-1}(1-p)& \text{für }n>k+1
\end{cases}
$$

Die Wahrscheinlichkeit, bei 2211 Lottorunden mit je 6.6 Millionen Tipps pro Runde mindestens einmal 7 Jackpots hintereinander zu bekommen erhalten wir, indem wir

$$1-P(2211,6,\left(1-\frac{1}{8145060}\right)^{6600000})$$

berechnen.

Tipps pro Runde

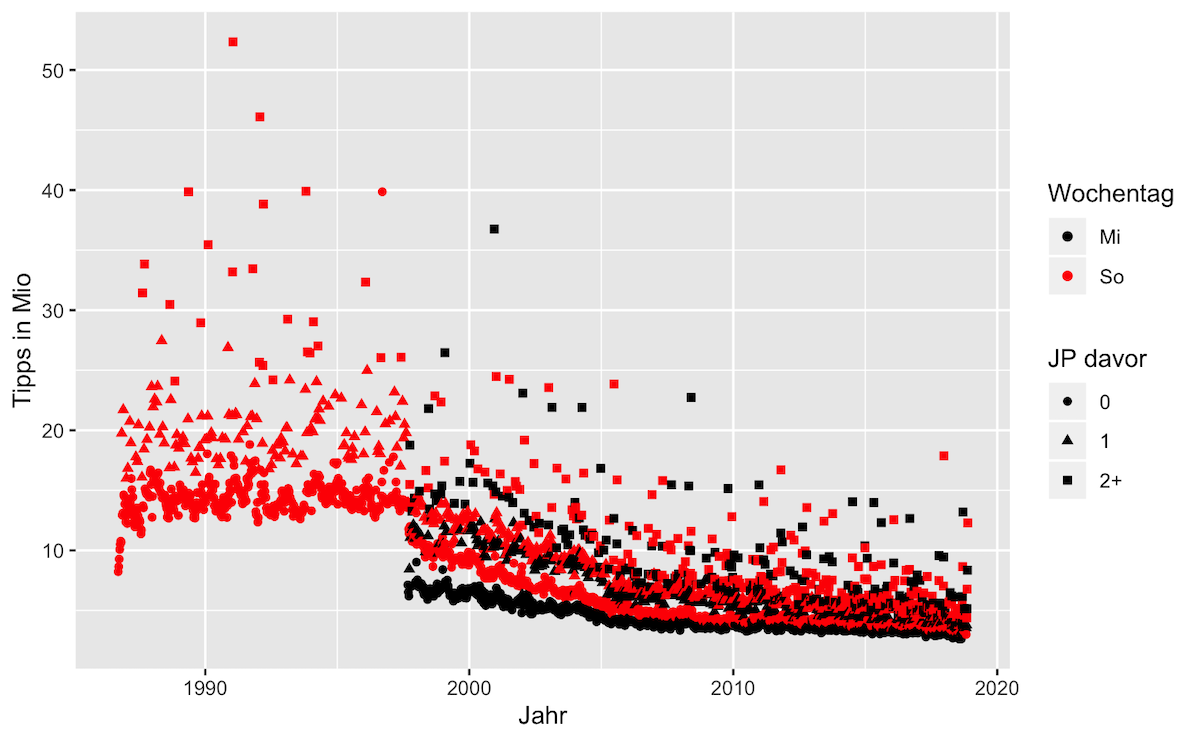
Die folgende Grafik zeigt die Entwicklung der Zahl der pro Runde abgegebenen Tipps:

Diese Zahlen sind nicht direkt publiziert. Publiziert sind aber die Gewinnhöhen und Gewinnerzahlen in den einzelnen Rängen. Außerdem findet man in den Spielbedingungen die Quoten, welcher Anteil der gesamten Lottoeinsätze in welchen Gewinntopf geht. Damit kann man die Tippzahlen ausrechnen.

Eine Simulation mit Jackpotwahrscheinlichkeiten

Man kann die Frage nach der Wahrscheinlichkeit des 7fach-Jackpots mit den sich nach der Jackpotanzahl ändernden Wahrscheinlichkeiten mit einer Simulation untersuchen. Macht man das mit den angegebenen Tippzahlen, dann erhält man für die Wahrscheinlichkeit bei 100.000 Serien der Länge 2211 einen Wert von 0,98.

Hier ist Code in der Programmiersprache R für diese Simulation

library(tidyverse)
library(magrittr)

tipps = c(3.0, 3.8, 4.4, 5.1, 6.8, 8.3, 12.3)*10^6
probs_no_6 <- (1-1/choose(45,6))^tipps

simul_eine_serie <- function(n,k){
  jackpots <- numeric(n)
  jackpots[1] <- 0
  for (i in 2:n){
    jackpots[i] <- ifelse(runif(1) <= (probs_no_6[jackpots[i-1]+1]),1+jackpots[i-1],0)
    if(jackpots[i] >= k) {break}
    }
  max(jackpots[1:i])
}

simulation <- function(repetitions,series_length,runlength){
  replicate(repetitions,simul_eine_serie(series_length,runlength)) %>%
    {table(.)[as.character(runlength)]/repetitions}
}

simulation(100000,2211,7)

Tipps bei Mehrfachjackpots

Die Zahl der abgegebenen Tipps steigt bei Mehrfachjackpots. Die Zahl der Tipps pro Runde hat aber auch mit Einführung der Mittwochziehungen (ab September 1997) abgenommen. Die folgende Tabelle zeigt die Anzahl der Tipps für diese verschiedenen Rahmenbedingungen.