Ein seltsames Schachproblem

Unter meinen regelmäßig erscheinenden mathematischen Puzzles (#mathepuzzle von @neuwirthe auf Twitter) ist auch folgendes:

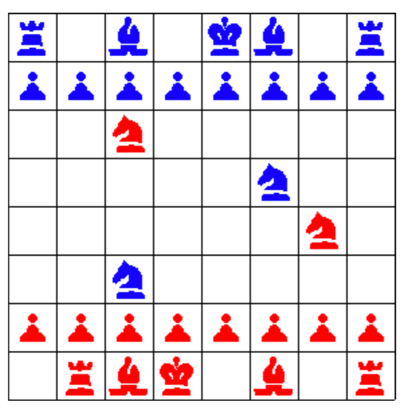
Auf dem abgebildeten Schachbrett gibt es rote und blaue Figuren.

Welche davon wären auf einem regulären Schachbrett und in einer korrekt nach den Schachregeln abgelaufenen Partie weiß und welche schwarz?
Wenn ihnen die Frage seltsam vorkommt, dann haben sie wahrscheinlich recht.

Es gibt aber tatsächlich eine eindeutige Lösung. Um sie zu finden muss man nicht gut Schach spielen können, sondern nur die Regeln kennen.
Wenn sie meinen, dass die Spieler keine besonders guten Spieler sind, haben sie ebenfalls recht. Die Stellung im Spiel wurde aber durch eine Folge regelkonformer Züge erreicht.

Wenn sie weiter scrollen, dann kommen sie zur Auflösung.

Relativ schnell sieht man, dass der blaue Springer in der 3. Reihe von unten dem roten König Schach gibt. Er muss also die letzte gezogene Figur sein. Was muss man noch wissen, damit man entscheiden kann ob er„logisch“ weiß oder schwarz ist?

Weiß hat immer den ersten (Halb-)Zug. In klassischer Schachsprechweise ist ein Zug nämlich immer die Bewegung einer weißen und danach einer schwarzen Figur, die Bewegung nur einer Figur heißt Halbzug.

Wenn wir die Halbzüge durchnummerieren, dann ist jeder ungerade Halbzug ein weißer und jeder gerade ein schwarzer Halbzug. Wenn wir also herausfinden, dass es insgesamt ungerade viele Halbzüge gegeben hat, dann wissen wir, dass die zuletzt gezogene Figur weiß war, und wenn die Zahl der Halbzüge gerade war, dann ist die letzte gezogene Figut eine schwarze.

Als allererstes stellen wir fest, dass die Bauern noch nicht bewegt wurden, denn sie können nicht verlustfrei Platz tauschen.

Danach fangen wir mit den blauen Türmen rechts und links oben an.
Beide stehen am ursprünglichen Aufstellungsort. Sie könnten sich jeweils um ein Feld nach innen und dann wieder nach außen bewegt haben, und das sogar mehrfach, die Anzahl der Halbzüge insgesamt ist da gerade.

Die roten Türme können sich auch jeweils nur um ein Feld seitlich bewegt haben. Der Turm links unten steht nicht auf seinem ursprünglichen Feld, er muss also eine ungerade Zahl von Halbzügen oft bewegt worden sein, der rechte muss (analog zu den roten) gerade oft bewegt worden sein. Insgesamt sind die Türme also ungerade oft bewegt worden.

Die Könige können sich (wie die Türme) ebenfalls nur ein Feld zur Seite bewegen. In der Startaufstellung steht der weiße König links von der weißen Dame, der schwarze König rechts von der schwarzen Dame. Sie stehen auf jeden Fall in derselben Spalte des Schacbretts. In unserer Stellung stehen sie in verschiedenen Spalten. Wir wissen nicht, welcher von beiden in der „falschen“ Spalte steht, aber der in der falschen Spalte muss ungerade oft gezogen worden sein, und der andere gerade oft. Beide zusammen müssen also ungerade oft gezogen worden sein.

Jetzt noch zu den Springern. Da hilft folgende Überlegung: Die Felder auf dem Schachbrett sind ja in einenm Diagonalmuster in zwei verschiedene Farben eingefärbt. Hier das Muster:

Springer der gleichen Farbe stehen zu Spielbeginn auf Feldern verschiedener Farbe, und jeder Springer wechselt bei jedem Halbzug von einem Feld einer Farbe zu einem Feld der anderen Farbe.
In unserer Problemstellung stehen die blauen Springer auf Feldern verschiedener Farbe, wurden also zusammen gerade oft bewegt. Die roten Springer stehen auf Feldern gleicher Farbe und wurden daher ungerade oft bewegt. Alle 4 Springer wurden zusammen also ungerade oft bewegt. Andere Figuren konnten nicht bewegt werden.

Die Bilanz aller Halbzüge lautet also: Türme ungerade, Könige ungerade, Springer ungerade. Insgsamt also ungerade viele Halbzüge.

Daher ist die letzte gezogene Figur, der blaue Springer in der 3. Reihe von unten, „logisch“ eine weiße Figur.

Hier noch ein paar Tweets, die zu dieser Aufgabe eingelangt sind:

In jedem ordentlichen Schachkaffee bekommt man für sowas auf Lebenszeit Lokalverbot… 😉

Beide Damen von Pferden gefressen, ohne dass die Bauern sich bewegt haette? Wie soll denn das zustande gekommen sein?

Himmel! Ich bin ein so schlechter Schachspieler, dass ich die Startaufstellung googlen musste. Die ist nicht rotationssymmetrisch. Dann ist rot schwarz.

Besonders gefreut hat mich das:

Und jetzt, wo es spannend wird, muss ich zum Einkauf! Wartet ihr bitte auf mich? 😉