Der Dominobogen
Wenn wir einen Dominostein seitlich verschoben auf einen anderen legen, dann können wir ihn fast um die halbe Länge nach rechts verschieben und er wird liegenbleiben und nicht herunterfallen.
Wenn wir noch einen weiteren (dritten) Stein drauflegen und wieder um fast die halbe Steinlänge verschieben, dann ist der schiefe Turm nicht mehr stabil und stürzt ein. Der Grund ist physikalisch. Der Schwerpunkt der beiden oberen Steine gemeinsam liegt nicht mehr innerhalb der Grundfläche des unteren Steins.
In unserem Fall sind die Steine alle 2.2 Einheiten lang. Der Schwerpunkt des untersten Steins liegt bei 0, der des mittleren Steins bei 1 und der des obersten Steins bei 2. Der mittlere und der obere Stein gemeinsam haben den Schwerpunkt bei 1.5 und das liegt außerhalb des rechtesten Punkts des untersten Steins (1.1). Der Turm knickt deshalb zwischen dem untersten und dem mittleren Stein ein.
Wie weit können wir denn den obersten Stein verschieben und doch noch einen stabilen Turm bekommen?
Da der 2. Stein den Spielraum schon fast ausreizt (Schwerpunkt bei 1, 1.1 wäre der schon fast instabile Grenzfall),
erscheint die Strategie, nur die Position des 3. Steins zu ändern, nicht ganz sinnvoll. Wir können auf jeden Fall den 3. Stein um 1 gegenüber dem 2. Stein verschieben, dann bleibt das Gesamtsystem aus 2. und 3. Stein stabil. Wenn wir jetzt dieses System etwas weniger weit verschieben, können wir einen stabilen Turm bauen.
Wenn der 3. Stein um 1 gegenüber dem 2. und der 2. Stein um $\frac{1}{2}$ gegenüber dem 1. Stein verschoben ist, dann haben der 2. und der 3. Stein gemeinsam einen Schwerpunkt von $\frac{\frac{1}{2}+(1+\frac{1}{2})}{2}=1$ und wir erhalten wieder einen stabilen Turm.
Wir können diesen 3er-Turm jetzt auf einen weiteren Stein stellen. Wie weit können wir denn diesen Turm gegen den Stein darunter verschieben und immer noch einen stabilen Turm erhalten?
Der Schwerpunkt des Turms aus 3 Steinen liegt bei
$\frac{0+\frac{1}{2}+(\frac{1}{2}+1)}{3}=\frac{2}{3}$, wir können den 3er-Turm also um $\frac{1}{3}$ gegenüber dem Stein darunter verschieben und erhalten immer noch einen stabilen 4er-Turm.
Probieren wir weiter: Der 4er-Turm hat den Schwerpunkt bei
$\frac{0+\frac{1}{3} + (\frac{1}{3}+\frac{1}{2})+(\frac{1}{3}+\frac{1}{2}+1)}{4}=\frac{3}{4}$,
wir können also diesen 4er-Turm auf einen weiteren Stein setzen und um $\frac{1}{4}$ verschieben und erhalten einen stabilen Turm der Höhe 5.
Das Prinzip funktioniert auch weiterhin. Bei einem Turm der Höhe $n$ nach dieser Bauart liegt der Schwerpunkt bei
$\frac{1}{n}$ und wir können ihn daher auf einen weiteren Stein draufsetzen und einen stabilen Turm der Höhe $n+1$ bauen.
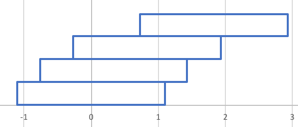
Der Überhang dieses Turmes ist dann $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n-1}$.
Ein nach diesem Prinzip gebauter Turm der Höhe 10 sieht so aus:
Die Summe wird beliebig groß (Mathematiker sagen „die Summe divergiert“). Das kann man so sehen:
$$1+\frac{1}{2}+\underbrace{\frac{1}{3}+\frac{1}{4}}_{\geq 2\cdot\frac{1}{4}=\frac{1}{2}}+\underbrace{\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}}_{\geq 4\cdot\frac{1}{8}=\frac{1}{2}} +
\underbrace{\frac{1}{9} + … + \frac{1}{16}}_{\geq 8\cdot\frac{1}{16}=\frac{1}{2}}…+…$$
Daher können wir jeden beliebigen Überhang erreichen. Allerdings brauchen wir dazu ziemlich viele Steine. Für einen Überhang von 10 brauchen wird 12367 Steine.
Mathematisches Postskriptum (nur für Nerds):
Dass alle Schwerpunkte die gewünschte Eigenschaften haben, zeigt man mit vollständiger Induktion.
Wenn $S(n)$ der Schwerpunkt eines Turmes der Höhe $n$ ist, dann gilt
$S(n+1)=\frac{n}{n+1}(\frac{1}{n}+S(n))$. Mit $S(2)=\frac{1}{2}$ gilt dann $S(n)=\frac{n-1}{n}$.
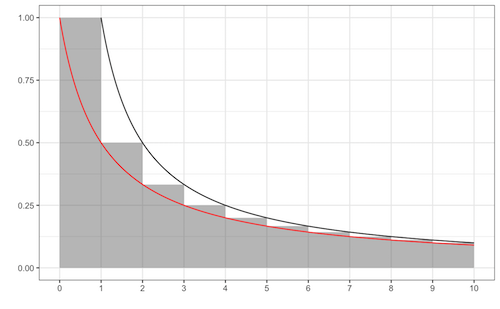
Mit Hilfe des grafischen Vergleichs der stetigen Funktionen $f(x)=\frac{1}{x}$ (schwarze Kurve) und $g(x)=\frac{1}{x+1}$ (rote Kurve) und der Sprungfunktion $h(x)=1/\lceil x \rceil$ (graue Blöcke)
und der Tatsache, dass der Logarithmus das unbestimmte Integral der Funktion $1/x$ ist, können wir eine Ungleichung über die Größe von $S(n)$ angeben.
$$\log(n+1) \leq S(n) \leq \log(n)+1$$
Durch Ungleichungsumformungen können wir daraus ableiten, dass für die Zahl $n$ der Steine, die notwendig sind, den Überhang $S$ zu erzielen, gilt:
$$e^{S-1} \leq n \leq e^S-1$$