Das Josephus-Problem
Eine genaue Beschreibung des Hintergrunds des Problems findet sich in der Wikipedia.
Problemstellung:
Eine bestimmte Zahl von Personen (n) steht im Kreis.
Es gibt eine „Startperson“. Geben wir ihr Nummer 1 und nummerieren wir fortlaufend im Kreis herum. Dann wird jede zweite Person aus dem Spiel genommen und zwar so lange, bis nur mehr eine Person übrig ist.
Bei 4 Personen werden also zunächst die Personen 2 und 4 aus dem Spiel genommen und wir sind wieder bei Person 1. Von dieser Startposition aus wird Person 3 aus dem Spiel genommen und 1 bleibt über.
Das gilt allgemeiner: Wann immer die Zahl der Personen gerade ist, dann ist man nach einer Runde genau wieder bei der ursprünglichen Startposition und das Verfahren wird fortgesetzt. Wenn die Zahl n eine Zweierpotenz ist (2, 4, 8, 16, …)ist, dann ist man nach jeder Runde an der Startposition und daher ist die Person an der Startposition auch die Person, die über bleibt.
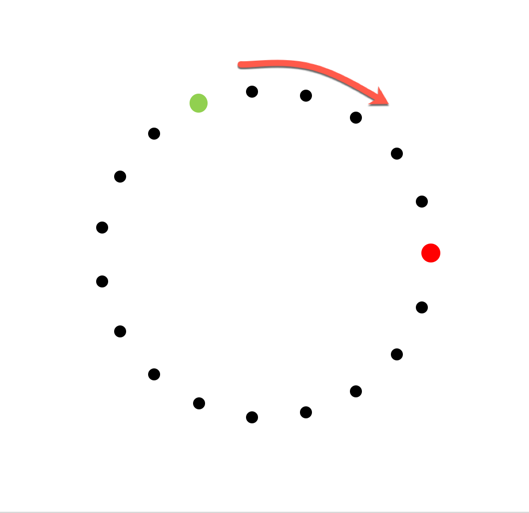
Bei den anderen Zahlen ist die Überlegung etwas komplizierter. Sehen wir uns den Fall n=19 an.
Wenn man das Spiel komplett zu Ende durchspielt, dann sieht man, dass von Startperson 1 aus gezählt Person 7 über bleibt.
Wir können auch sagen: Bei 19 Personen ist die Person 6 Positionen vor der Startperson die, die über bleibt. (Vor bedeutet in Pfeilrichtung.)
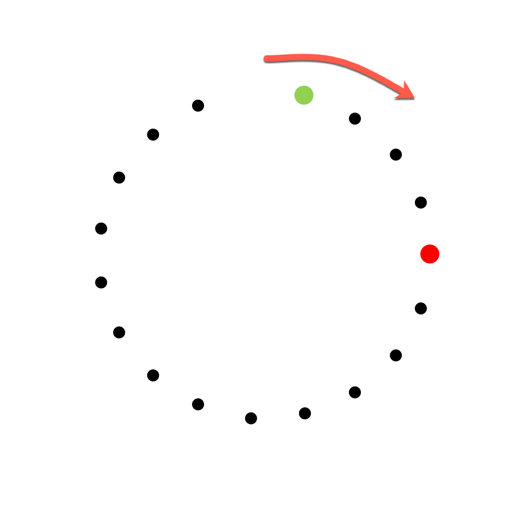
Wenn wir jetzt einen einzelnen Schritt des Ausscheidungsverfahrens durchführen, dann sehen wir folgendes Bild:
Wir haben eine neue Konfiguration mit n=18 und einer neuen Startposition. Die vorher und nachher rot markierte Position ist in beiden Fällen die Position der Person, die über bleibt.
Diese „Überbleibposition“ ist in der neuen Konfiguration 4 Schritte, also 2 Schritte weniger als in der alten Konfiguration von der Startposition entfernt. Das gilt fast immer, es gibt nur 2 mögliche Ausnahmen. Wenn die Startposition und die Überbleibposition identisch sind, dann funktioniert diese Überlegung nicht. Wenn die Überbleibposition nur einen Schritt hinter der Startposition läge, dann würde das ebenfalls nicht funktionieren. Die Position unmittelbar hinter der Startposition kann aber nie die Endposition sein, da die Person dort ja auf jeden Fall im nächsten Schritt entfernt wird.
Wir können diese Überlegung auch in umgekehrter Richtung anwenden. Wenn eine Position dazukommt, dann erhöht sich der Abstand zur Überbleibposition um 2.
Wir wissen also: Wenn n eine Zweierpotenz ist, dann ist die Startpostion auch die Überbleibposition.
Damit können wir die Überbleibposition für alle Fälle bestimmen. Für Zweierpotenzen ist 1 die Lösungszahl, und für jede
zusätzliche Position wird die Lösungszahl um 2 erhöht (wir müssen ja um 2 Positionen weitergehen). Sobad wir beim Dazugeben von Positionen zur nächsten Zweierpotenz kommen starten wir wieder mit Lösungszahl 1.
| Positionen | bleibt über |
| 1 | 1 |
| 2 | 1 |
| 3 | 3 |
| 4 | 1 |
| 5 | 3 |
| 6 | 5 |
| 7 | 7 |
| 8 | 1 |
| 9 | 3 |
| 10 | 5 |
| 11 | 7 |
| 12 | 9 |
| 13 | 11 |
| 14 | 13 |
| 15 | 15 |
| 16 | 1 |
| 17 | 3 |
| 18 | 5 |
| 19 | 7 |
| 20 | 9 |
Didaktische Nachbemerkung
Es gibt mehrere Möglichkeiten, die Lösung mathematisch abzuleiten und zu begründen. Die bekannteste davon findet sich im Buch „Concrete Mathematics“ von Donald Knuth, Ron Graham und Oren Patashnik. Eine andere Erklärung der Lösung mit einer sehr netten Animation gibt es bei Numberphile auf YouTube.
Bei beiden Erklärungen gibt es keine unmittelbar einleuchtende Begründung dafür, warum in den meisten Fällen eine zusätzliche Person die Lösungszahl um zwei erhöht. Hauptgrund ist, dass man in beiden Ansätzen über die Nummerierung der Personen, also einen absoluten Bezug spricht. Im obigen Ansatz spielt der Abstand zwischen Startposition und Endposition die wichtigste Rolle, und das ist ein relativer, kein absoluter Bezug. Mein Eindruck ist, dass dieser Wechsel des Beschreibungssystems den Lösungsweg leichter verständlich macht.
2 Comments
1) Bei 19 Personen ist die Person 6 Positionen vor der Startperson die, die über bleibt.
-> muss das nicht „hinter“ statt „vor“ heißen?
Ok, nochmaliges Durchlesen zeigt: „vor“ bzw. „hinter“ sind hier nicht ganz klar definiert.
2) Diese „Überbleibposition“ ist in der neuen Konfiguration 6 Schritte, also 2 Schritte weniger als in der alten Konfiguration von der Startposition entfernt.
-> muss das nicht (statt 6) „4 Schritte“ heißen?
Danke, jetzt ausgebessert.