Österreichs Gymnasiasten und Finnlands Gesamtschüler
Eines der gelegentlich verwendeten Argumente in der Diskussion „Gesamtschule ja oder nein“ lautet ungefähr so:
Um die Rolle des Gymnasiums (beziehungsweise der AHS) in unserem Bildungssystem richtig einzuschätzen sollte man wissen, dass die Ergebnisse, die unsere AHS-Schüler bei PISA erreichen, schlechter sind als die aller finnischen Schüler zusammengenommen.
Wenn dieses Argument richtig wäre, dann wäre es zumindest ein starkes Argument gegen die Beibehaltung der AHS in der gegenwärtigen Gestalt. Daher wollen wir uns die Daten genauer ansehen.
Die folgende Tabelle zeigt die PISA Ergebnisse in den 3 Gebieten Lesen, Mathematik und Naturwissenschaften für alle vier bisherigen PISA-Testserien (2000, 2003, 2006, 2009). Ausgewiesen werden die Durschnittsscores für alle finnischen Schüler, für die österreichischen AHS-Schüler, für die österreichischen BHS-Schüler und für alle österreichischen Schüler.
| Jahr | Schüler | Lesen | Mathe | Naturw. |
|---|---|---|---|---|
| 2000 | Finn alle | 546.5 | 536.2 | 537.7 |
| Ö AHS | 564.2 | 564.2 | 571.8 | |
| Ö BHS | 544.3 | 552.6 | 556.0 | |
| Ö alle | 492.1 | 502.5 | 504.7 | |
| 2003 | Finn alle | 543.5 | 544.3 | 548.2 |
| Ö AHS | 571.6 | 570.7 | 566.1 | |
| Ö BHS | 544.7 | 553.5 | 540.2 | |
| Ö alle | 490.7 | 505.6 | 491.0 | |
| 2006 | Finn alle | 546.9 | 548.4 | 563.3 |
| Ö AHS | 568.6 | 568.5 | 578.1 | |
| Ö BHS | 541.5 | 553.1 | 558.1 | |
| Ö alle | 490.2 | 505.5 | 510.8 | |
| 2009 | Finn alle | 535.9 | 540.5 | 554.1 |
| Ö AHS | 550.4 | 568.0 | 568.3 | |
| Ö BHS | 515.7 | 541.6 | 540.3 | |
| Ö alle | 470.3 | 495.9 | 494.3 |
Die österreichischen AHS-Schüler hatten also bei allen bisherigen PISA-Tests in allen 3 getesteten Bereichen immer deutlich bessere Durchschnittswerte als die finnischen Schüler, der Abstand betrug nie weniger als 14 Punkte.
Die Werte für PISA 2000 in Österreich in dieser Tabelle unterscheiden sich von den in den offiziellen internationalen und österreichischen PISA-Publikationen für 2000 und 2003 ausgewiesenen Werten. Eine Arbeitsgruppe aus österreichischen Statistikern hat 2005 methodische Probleme bei PISA 2000 bereinigt und die OECD verwendet seit 2006 die nach den dabei entwickelten Verfahren korrigierten Werte als offizielles österreichisches Ergebnis für das Jahr 2000.
Die AHS ist aber nicht die einzige Schulform in Österreich, die mit der Hochschulreife abschließt, das tut auch die BHS. Deswegen sind in den Tabellen dieses Postings immer auch die Ergebnisse der BHS ausgewiesen. Die bewegen sich etwa im Bereich der finnischen Ergebnisse. Bei PISA 2009 sind sie schlechter, aber diese Werte wurden während eines bildungspolitisch negativ aufgeladenen Zeitraums erhoben und sind deswegen nur bedingt aussagekräftig.
In den bildungspolitischen Diskussionen taucht noch ein weiteres Argument, warum das österreichische Gymnasiums die gestellten Anforderungen nicht erfüllt, auf.
PISA definiert „top performers“, also Schüler, die Spitzenleistungen erbringen. Ein Vorwurf an das Gymnasium lautet, dass es dort weniger Spitzenschüler gibt als in Finnland.
Wir analysieren daher die Tabelle mit den Anteilen der Spitzenschüler in den 3 Testbereichen und dazu noch den Anteilen aller Schüler, die in allen 3 Bereichen beziehungsweise in mindestens einem der drei Bereiche Spitzenleistungen erbringen.
| Jahr | Schüler | Lesen Top | Mathe Top | Naturw. Top | Alles Top | Mind. 1 Top |
|---|---|---|---|---|---|---|
| 2000 | Finn alle | 18.1% | 19.1% | 13.3% | ||
| Ö AHS | 18.8% | 29.1% | 20.7% | |||
| Ö BHS | 10.9% | 23.1% | 13.8% | |||
| Ö alle | 7.3% | 13.5% | 8.5% | |||
| 2003 | Finn alle | 14.3% | 23.4% | 17.5% | 7.6% | 30.9% |
| Ö AHS | 22.6% | 31.0% | 17.8% | 9.3% | 40.9% | |
| Ö BHS | 11.1% | 24.4% | 9.6% | 4.4% | 29.2% | |
| Ö alle | 8.1% | 14.3% | 6.6% | 3.2% | 17.9% | |
| 2006 | Finn alle | 16.4% | 24.4% | 20.9% | 9.4% | 32.7% |
| Ö AHS | 23.4% | 31.7% | 22.5% | 11.8% | 42.3% | |
| Ö BHS | 10.2% | 24.2% | 14.7% | 5.4% | 29.2% | |
| Ö alle | 8.8% | 15.8% | 10.0% | 4.3% | 20.2% | |
| 2009 | Finn alle | 14.2% | 21.7% | 18.7% | 8.4% | 29.3% |
| Ö AHS | 14.2% | 31.0% | 19.3% | 8.6% | 36.5% | |
| Ö BHS | 5.2% | 18.5% | 11.5% | 3.0% | 21.8% | |
| Ö alle | 4.8% | 12.9% | 8.0% | 2.9% | 15.3% |
Warum gibt es in dieser Tabelle leere Zellen?
Bei PISA 2000 stehen die Werte für Mathematik und Naturwissenschaften nicht für alle Schüler zur Verfügung, daher ist eine gemeinsame Auswertung der Scores wie ab PISA 2003 nicht möglich.
Auch in dieser Tabelle sind alle Anteile der Spitzenschüler bei den österreichischen AHS-Schülern niemals geringer als der entsprechenden Anteil an allen finnischen Schülern.
Berücksichtigt man die Tatsache, dass die Schüler in österreichischen AHS nach den Leistungen in der Volksschule selektiert werden, dann darf man natürlich fragen, ob man insbesondere beim Anteil der Spitzenschüler in der österreichischen AHS deutlich bessere Werte erzielen sollte als die finnische Gesamtschule.
Das gelegentlich vorgebrachte Argument, dass die österreichische AHS trotz Selektion nicht einmal die Leistungen der finnischen Gesamtschule ohne Selektion erbringt, ist also mit den PISA-Daten nicht zu untermauern. Sowohl bei der Durchschnittsleistung als auch beim Anteil der Spitzenschüler schneidet die österreichische AHS besser ab als die finnische Schule.
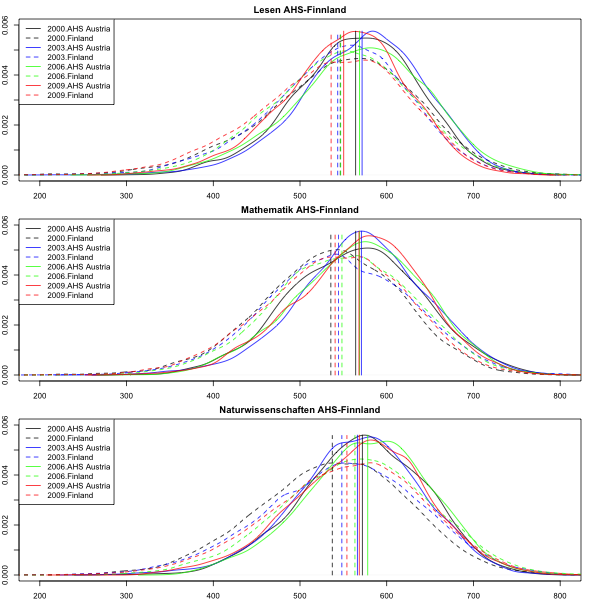
Eine so grosse Menge von Daten wie die Scores alle PISA-getesteten Schüler stellen Statistiker auch grafisch dar, und zwar mit Dichtefunktionen. Die folgende Grafik zeigt
die Verteilung des Scores für alle finnischen Schüler und für die österreichischen AHS-Schüler.
Die Farbe der Kurven gibt den Testzeitpunkt an. Die Höhe der Kurve gibt an, ob sich im die Testwerte der Schüler in entsprechenden Bereich häufig oder selten waren. Man kann also ablesen, dass im Bereich um den Score 600 in Mathematik bei allen PISA-Tests etwa 30-50% mehr österreichische AHS-Schüler als finnische Schüler zu finden sind. Die senkrechten Striche geben die Mittelwerte aller Scores, also die von der OECD als PISA-Score der Länder publizierten Werte an. Diese Werte findet man auch in der weiter oben stehenden Tabelle. Die Mittelwerte für die österreichischen
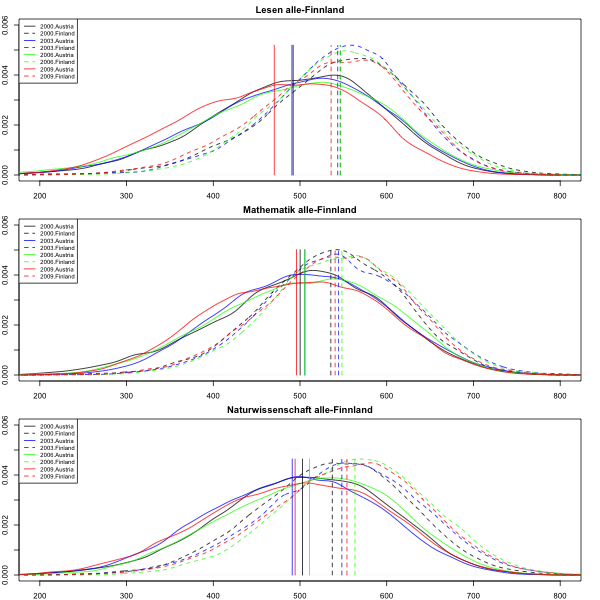
AHS-Schüler liegen in den meisten Fällen deutlich rechts von den entsprechenden Werten der finnischen Schüler, die Durchschnittsleistung der AHS-Schüler ist also in der Regel deutlich besser als die der finnischen Schüler. Zum Vergleich die Grafik, die alle österreichischen Schüler allen finnischen Schülern gegenüberstellt.
Die österreichischen Kurven liegen deutlich links von den entsprechenden finnischen Kurven, die österreichischen Gesamtergebnisse sind also deutlich schlechter. Das gilt auch für die senkrechten Linien, also die Länderscores. Aber das wissen wir ja schon lange.
Methodische Anmerkungen
Bei statistischen Auswertungen wie PISA gehört zur statistisch sauberen Durchführung auch, dass man zu jedem geschätzten Wert einen Schwankungsbereich angibt. Üblich ist das 95%-Konfidenzintervall. Daher sehen sie hier noch einmal die Tabelle der PISA-Scores ergänzt mit den Schwankungsbereichen.
| Jahr | Schüler | Lesen | Mathe | Naturw. |
|---|---|---|---|---|
| 2000 | Finn alle | 546.5 ± 5.1 | 536.2 ± 2.1 | 537.7 ± 2.5 |
| Ö AHS | 564.2 ±10.6 | 564.2 ± 5.4 | 571.8 ± 4.6 | |
| Ö BHS | 544.3 ± 8.2 | 552.6 ± 5.5 | 556.0 ± 5.9 | |
| Ö alle | 492.1 ±5.3 | 502.5 ± 2.7 | 504.7 ± 2.7 | |
| 2003 | Finn alle | 543.5 ± 3.2 | 544.3 ± 1.9 | 548.2 ± 1.9 |
| Ö AHS | 571.6 ±11.3 | 570.7 ± 6.5 | 566.1 ± 5.9 | |
| Ö BHS | 544.7 ± 7.2 | 553.5 ± 4.0 | 540.2 ± 3.6 | |
| Ö alle | 490.7 ± 7.4 | 505.6 ± 3.3 | 491.0 ± 3.4 | |
| 2006 | Finn alle | 546.9 ± 4.2 | 548.4 ± 2.3 | 563.3 ± 2.0 |
| Ö AHS | 568.6 ± 8.5 | 568.5 ± 5.3 | 578.1 ± 4.8 | |
| Ö BHS | 541.5 ± 7.3 | 553.1 ± 4.6 | 558.1 ± 4.2 | |
| Ö alle | 490.2 ± 8.0 | 505.5 ± 3.7 | 510.8 ± 3.9 | |
| 2009 | Finn alle | 535.9 ± 4.4 | 540.5 ± 2.2 | 554.1 ± 2.3 |
| Ö AHS | 550.4 ±11.3 | 568.0 ± 4.7 | 568.3 ± 5.2 | |
| Ö BHS | 515.7 ± 8.4 | 541.6 ± 5.1 | 540.3 ± 5.2 | |
| Ö alle | 470.3 ± 5.8 | 495.9 ± 2.7 | 494.3 ± 3.2 |
Hier die Tabelle der Spitzenschüleranteile, ebenfalls mit den Schwankungsbereichen.
| Jahr | Schüler | Lesen Top | Mathe Top | Naturw. Top | Alle Top | Mind. 1 Top |
|---|---|---|---|---|---|---|
| 2000 | Finn alle | 18.1% ±1.8% | 19.1% ±1.8% | 13.3% ±1.7% | ||
| Ö AHS | 18.8% ±5.2% | 29.1% ±6.6% | 20.7% ±4.6% | |||
| Ö BHS | 10.9% ±2.6% | 23.1% ±4.7% | 13.8% ±3.7% | |||
| Ö alle | 7.3% ±1.4% | 13.5% ±1.9% | 8.5% ±1.4% | |||
| 2003 | Finn alle | 14.3% ±1.4% | 23.4% ±1.6% | 17.5% ±1.6% | 7.6% ±1.2% | 30.9% ±1.7% |
| Ö AHS | 22.6% ±5.1% | 31.0% ±5.8% | 17.8% ±4.6% | 9.3% ±3.2% | 40.9% ±6.7% | |
| Ö BHS | 11.1% ±2.8% | 24.4% ±3.5% | 9.6% ±2.5% | 4.4% ±1.7% | 29.2% ±4.1% | |
| Ö alle | 8.1% ±1.5% | 14.3% ±1.9% | 6.6% ±1.4% | 3.2% ±0.8% | 17.9% ±2.3% | |
| 2006 | Finn alle | 16.4% ±1.7% | 24.4% ±2.0% | 20.9% ±1.5% | 9.4% ±1.0% | 32.7% ±1.9% |
| Ö AHS | 23.4% ±4.0% | 31.7% ±5.0% | 22.5% ±4.1% | 11.8% ±2.1% | 42.3% ±5.5% | |
| Ö BHS | 10.2% ±2.5% | 24.2% ±3.9% | 14.7% ±3.0% | 5.4% ±2.1% | 29.2% ±4.1% | |
| Ö alle | 8.8% ±1.3% | 15.8% ±1.9% | 10.0% ±1.5% | 4.3% ±0.7% | 20.2% ±2.3% | |
| 2009 | Finn alle | 14.2% ±1.4% | 21.7% ±1.8% | 18.7% ±1.8% | 8.4% ±1.2% | 29.3% ±2.0% |
| Ö AHS | 14.2% ±3.8% | 31.0% ±4.1% | 19.3% ±3.2% | 8.6% ±2.5% | 36.5% ±4.8% | |
| Ö BHS | 5.2% ±2.0% | 18.5% ±3.9% | 11.5% ±3.3% | 3.0% ±1.4% | 21.8% ±4.0% | |
| Ö alle | 4.8% ±1.0% | 12.9% ±1.7% | 8.0% ±1.2% | 2.9% ±0.7% | 15.3% ±1.7% |
Warum enthält diese Tabelle leere Zellen?
Die PISA-Methodik wird ständig weiter entwickelt. Bei PISA 2000 wurden nicht für alle Schüler Mathematik- und Naturwissenschaftsscores errechnet. Deshalb sind die Schätzungen der Anteile von Schülern mit Spitzenleistungen in mehreren Gebieten mit der selben methodischen Zuverlässigkeit wie bei den späteren PISA-Tests nicht möglich.
1 Comment
[…] dem schon vor einiger Zeit publizierten Blog-Eintrag “Österreichs Gymnasiasten und Finnlands Gesamtschüler” sind einige Grafiken dazugekommen. Die machen einige Sachverhalte noch deutlicher sichtbar als die […]