Puzzle: Überlappende Quadrate

Auf Twitter habe ich folgendes Puzzle publiziert:

In einem Quadrat mit 1 m Seitenlänge werden 2 Quadrate mit 1/2 m Seitenlänge an zufälligen Stellen gezeichnet. Die kleineren Quadrate liegen innerhalb des großen Quadrats.
Die Seiten der kleineren Quadrate sind parallel (bzw. im rechten Winkel) zu den Seiten des großen Quadrats.
Wie groß ist die Wahrscheinlichkeit, dass die beiden kleineren Quadrate überlappen?
Wie groß ist die Wahrscheinlichkeit, wenn die kleineren Quadrate
die Seitenlänge 1/3 m haben? Und wie groß bei 1/4 m?

Gefunden habe ich dieses Puzzle auf der Website https://www.braingle.com/brainteasers/

Im folgenden Applet kann man die Quadrate verschieben (an den blau markierten Mittelpunkten).
Die Seitenlänge der Quadrate kann man mit den Schieberegler ganz oben verändern.

Bei einer Seitenlänge von 1/2 m überlappen die Quadrate nur dann nicht, wenn eines davon ganz ab der Oberkante des großen Quadrats und das andere an der Unterkante anliegt, oder wenn eines an der rechten und das andere an der linken Kante des großen Quadrats anliegt. Wenn beide kleineren Quadrate zufällig zu liegen kommen, dann ist die Wahrscheinlichkeit dafür 0. In allen anderen Konfigurationen überlappen sie, daher ist die Wahrscheinlichkeit fürs Überlappen 1.

Wenn die Seitenlänge der kleineren Quadrate größer als 1/2 m ist und beide im großen Quadrat liegen, dann überlappen sie immer.

Damit bleibt nur der Fall, dass die Seitenlänge kleiner als 1/2 ist. (Wir lassen ab jetzt die Maßeinheit m weg).

Wenn ein kleines Quadrat innerhalb des großen Quadrats liegt, dann ist der Mittelpunkt des Quadrats mindestes eine halbe Seitenlänge von der oberen und der unteren Seite des großen Quadrats entfernt (senkrecht gemessen), und ebenso mindestens eine halbe Seitenlänge von der rechten und der linken Seite (waagrecht gemessen). Der Mittelpunkt eines kleinen Quadrats liegt also in einem Quadrat mit Seitenlänge $1-s$ innerhalb des großen Quadrats. Mit der Checkbox „Grenze für Mittelpunkte“ wird dieses Quadrat im Applet oben sichtbar.

Die beiden kleinen Quadrate überlappen genau dann, wenn der Abstand ihrer Mittelpunkte waagrecht gemessen und senkrecht gemessen jeweils kleiner ist als die Seitenlänge der Quadrate.
Wenn man die Checkbox „Abstände“ aktiviert, dann werden diese beiden Abstände angezeigt und grün oder rot gefärbt, je nachdem, ob sie größer oder kleiner als die Seitenlänge sind.

Damit können wir die ursprüngliche Aufgabe umformulieren, nämlich so:
Wie groß ist die Wahrscheinlichkeit, dass zwei in einem Quadrat der Seitenlänge $1-s$ zufällig gewählte Punkte sowohl waagrecht als auch senkrecht einen Abstand von weniger als $s$ haben.

Bei zufälliger Wahl von zwei Punkte in einem Quadrat sind die senkrechten und die waggrechten Abstände voneinander unabhängig.
Wir berechnen daher die Wahrscheinlichkeit dafür, dass zwei zufällig auf einer Strecke der Länge $1-s$ gewählte Punkte einen Abstand von weniger als $s$ haben.
Diese Wahrscheinlichkeit gilt dann sowohl für die waagrechten als auch für die senkrechten Abstände. Als Folge ist das Quadrat dieser Wahrscheinlichkeit die Wahrscheinlichkeit, die wir suchen, nämlich dass die zwei Mittelpunkte sowohl waagrecht als auch senkrecht einen Abstand von weniger als $s$ haben.

Das folgende Applet hilft dabei, die Wahrscheinlichkeit für die Punkte auf der Strecke zu berechnen.
Die Punkte $x$ und $y$ können mit der Maus verschoben werden.
Die Strecke zwischen $x$ und $y$ ändert die Farbe
je nach dem Abstand der beiden Punkte. Sie ist grün, wenn der Abstand kleiner als $s$ ist und rot, wenn der Abstand größer oder gleich $s$ ist. Das rot-grüne Quadrat hat die Seitenlänge $1-s$.

$y’$ ist der an der Diagonale gespiegelte Punkt $y$.
Man erkennt, dass der Abstand zwischen $x$ und $y$ genau dann kleiner als $s$ ist, wenn der Punkt $(x,y)$ im grünen Teilbereich des Quadrats liegt.
Die Wahrscheinlichkeit, dass der Abstand zwischen $x$ und $y$ kleiner als $s$ ist, ist daher der Anteil der grünen Fläche an der Gesamtfläche des Quadrats.

Das gesamte Quadrat hat die Fläche $(1-s)^2$.
Die beiden roten Dreiecke bilden zusammengelegt ein Quadrat mit der Seite $1-2s$, also ist die rote Fläche $(1-2s)^2$.
Die grüne Fläche ist daher $(1-s)^2-(1-2s)^2=s(2-3s)$
Der Anteil der grünen Fläche an der Quadratfläche ist also $\frac{s(2-3s)}{(1-s)^2}$

Das ist die Wahrscheinlichkeit, dass zwei zufällig gewählte Punkte auf einer Strecke der Länge $1-s$ einen Abstand von weniger als $s$ haben.

Für die ursprüngliche Aufgabe müssen sowohl der waagrechte als auch der senkrechte Abstand der Quadratmittelpunkte kleiner als $s$ sein, daher müssen wir
die Wahrscheinlichkeiten für waagrecht und für senkrecht miteinander multiplizieren.

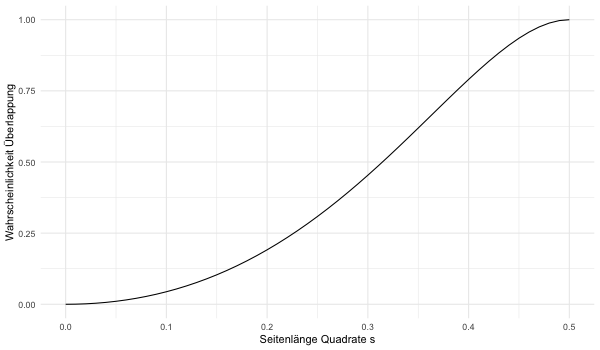
Die Wahrscheinlichkeit, dass die beiden Quadrate des ursprünglichen Problems überlappen, beträgt daher

$$
\left(\frac{s(2-3s)}{(1-s)^2}\right)^2
$$

Für $s=\frac{1}{3}$ ergibt das $\frac{9}{16}=0.563$ und für $s=\frac{1}{4}$ ergibt das $\frac{25}{81}=0.309$

Die Wahrscheinlichkeit für alle Werte von $s$ zwischen 0 und $\frac{1}{2}$ zeigt folgendes Schaubild: