Wieviele 6-stellige Zahlen kann man mit 4 Ziffern schreiben?
Ein bisschen kombinatorisches Denken
Ich habe unlängst in meiner Twitterserie #mathepuzzle folgende Aufgabe gestellt:132324 ist eine 6-stellige Zahl, in der nur 4 verschiedene Ziffern vorkommen. Nennen wir so etwas eine 6-stellig 4-ziffrige Zahl. Wieviele 6-stellige 1-ziffrige, 2-ziffrige, …, 5-ziffrige und 6-ziffrige Zahlen gibt es? Führende Nullen sind erlaubt.Wie kann man das herausfinden? Mathematiker neigen dazu, solche Probleme gleich allgemeiner anzugehen. Überlegen wir also, welche verwandten Fälle wir leicht lösen können.
1-stellig 1-ziffrig ist einfach, da gibt es genau die 10 Zahlen 0, 1, 2, …, 9
2-stellig 1-ziffrig geht auch nur 10x, 00, 11, 22, … 99 und das gilt für eine beliebige Zahl von Stellen. Es gibt für jedes $n$ 10 $n$-stellig 1-ziffrige Zahlen; wir können ja jede $n-1$-stellige 1-ziffrige Zahl nur unter Verwendung der einen bereits verwendeten Ziffer zu einer $n$-stelligen 1-ziffrigen Zahl verlängern. Wir wissen also jetzt, dass es 10 2-stellige 1-ziffrige Zahlen gibt. Da es insgesamt 100 2-stellige Zahlen gibt, gibt es 90 2-stellig 2-ziffrige Zahlen. Wir können die Anzahl der Zahlen mit lauter verschiedenen Ziffern für jede beliebige Stellenzahl ausrechnen. Für die erste Stelle gibt es 10 Möglichkeiten, jede dieser 1-stelligen Zahlen kann auf 9 Arten zu einer 2-stellig 2-ziffrigen Zahl verlängert werden.
Jede dieser 90 2-stellig 2-ziffrigen Zahlen kann auf 8 Arten zu einer 3-stellig 3-ziffrigen Zahl verlängert werden, also gibt es $10\cdot 9\cdot 8=720$ 3-stellig 3-ziffrige Zahlen.
4-stellig 4-ziffrige Zahlen gibt es daher $10\cdot 9\cdot 8\cdot 7=5040$, und dieses Rechenrezept können wir bis zu 10-stelligen Zahlen verwenden. 11-stellige Zahlen mit lauter verschiedenen Ziffern kann es ja nicht geben, wenn nur 10 Ziffern zur Verfügung stehen. Das gilt auch für viele anderer Fälle: Es gibt keine Zahlen, die mehr verschiedene Ziffern verwenden als sie Stellen haben. Wir wissen jetzt, dass 10 3-stellig 1-ziffrige und 720 3-stellig 3-ziffrige Zahlen gibt. Daher gibt es $1000-10-720=270$ 3-stellig 2-ziffrige Zahlen.
Wir können das, was wir uns bisher überlegt haben, in einer Tabelle zusammenfassen:
Jetzt stellen wir eine neue Reihe mit 6 Schachteln (wieder nummeriert von 1 bis 6) auf. Dann erzeugen wir von jedem Zettel in Schachtel 1 (aus der Reihe für die 3-stelligen Zahlen) 10 Kopien und hängen an die 3-stellige Zahl jeweils eine der 10 Ziffern an. So entstehen 4-stellige Zahlen. Diese Zahlen legen wir in die „richtigen“ Schachteln für die 4-stelligen Zahlen. Wenn wir die 2-stellig 1-ziffrigen Zahlen mit jeweils einer Ziffer verlängern (z.B. 111), dann bekommen wir 1 4-stellig 1-ziffrige Zahl (nämlich 1111) und 9 4-stellig 2-ziffrige Zahlen (1111, 1112, 1113, …, 1119, 1110). Eine unserer verlängerten Zahlen hat also die gleich „Ziffrigkeit“ und bei 9 verlängerten Zahlen wird die Ziffrigkeit um 1 höher.
Wenn wir 3-stellig 2-ziffrige Zahlen (z.B. 121) mit allen 10 möglichen Ziffern verlängern, dann sind 2 der Verlängerungen wieder 2-ziffrig (1211 und 1212) und die übrigen 8 Verlängerungen sind 3-ziffrig. Wir haben also aus den 10 3-stellig 1-ziffrigen Zahlen 90 4-stellig 2-ziffrige Zahlen erzeugt, und aus den 270 3-stellig 2-ziffrigen ebenfalls $2\cdot 270=540$ 4-stellig 2-ziffrige Zahlen, insgesamt also $9\cdot 10+2\cdot 270=630$ 4-stellig 2-ziffrige Zahlen. Es gibt ja keine andere Art, solche Zahlen durch Verlängerung 3-stelliger Zahlen zu erzeugen, daher sind das alle derartigen Zahlen. Mit den gleichen Überlegungen können wir sehen, dass wir alle 4-stellig 3-ziffrigen Zahlen aus den 3-stellig 2-ziffrigen und den 3-stellig 3-ziffrigen erzeugen können. Jede 3-stellig 2-ziffrige Zahl kann auf 8 Arten zu einer 4-stellig 3-ziffrigen verlängert werden (wir hängen einfach hinten eine der 8 noch nicht verwendeten Ziffern an), und jede 3-stellig 3-ziffrige Zahl kann auf 3 Arten zu einer 4-stellig 3-ziffrigen Zahl verlängert werden, indem wir jeweils eine der 3 schon verwendeten Ziffern hinten anhängen.
Es gibt daher $8\cdot 270+3\cdot 720=3600$ 4-stellig 3-ziffrige Zahlen.
Das Rezept funktioniert auch für die 4-stellig 4-ziffrigen Zahlen: Jede 3-stellig 3-ziffrige Zahl kann auf 7 Arten (mit einer der $10-3$ noch nicht verwendeten Ziffern) zu einer 4-stellig 4-ziffrigen Zahl erweitert werden. 3-stellig 4-ziffrige Zahlen gibt es nicht, daher ist der zweite Ausdruck in der Summe, die wir typischerweise berechnen, einfach 0. In unserer Tabelle können wir das Muster unserer Rechnung so beschreiben: in jeder Zelle steht eine Summe aus 2 Produkten. Das erste Produkt ist die Zahl links darüber multipliziert mit (10-Spaltennummer) der Spalte, aus der diese Zahl kommt, das zweite Produkt ist die Zahl unmittelbar darüber multipliziert mit der Spaltennummer dieser Spalte.
Diese Rechnung gilt für alle 2- oder mehrstelligen und 2- oder mehrziffrigen Zahlen. Die so vervollständigte Tabelle sieht so aus:
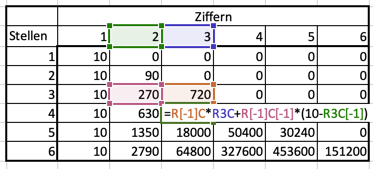
rosa . grün + orange . blau. Die Formelschreibweise ist vielleicht nicht die, die sie normalerweise in Excel sehen. Man kann sie aber in den Excel-Optionen einschalten. R[-1]C bedeutet beispielsweise Zeile (englisch row) darüber, selbe Spalte (englisch column). Wenn ihr Excel auf deutsch eingestellt ist, dann steht dort Z[-1]SZ3S+Z[-1]S[-1]Z3S[-1] Wir sehen in dieser Tabelle, dass es 327600 6-stellige 4-ziffrige Zahlen gibt. Übersetzt in die „übliche“ mathematische Schreibweise lautet die Lösung unseres Problem so: $$F(1,1)=10\\
F(n,1)=10 \text{ für } n>1 \\
F(1,k) = 0 \text{ für } k>1 \\
F(n,k) = (10-(k-1))F(n-1,k-1)+k F(n-1,k)\text{ sonst}
$$ $F(n,k)$ ist dabei die Zahl in der Zelle mit Zeilennummer $n$ und Spaltennummer $k$. Die Formel ist also inhaltlich vollkommen gleich mit der verbalen Beschreibung der Tabelle; sie drückt das Rechenrezept nur in der in der Mathematik üblichen sehr kompakten Schreibweise aus. Zusatzanmerkung:
Wir haben die Anzahl der Zahlen mit lauter verschiedenen Ziffern als $10$, $10 \cdot 9$, $10 \cdot 9 \cdot 8$ usw. berechnet. Diese Zahlen sind strukturell Potenzen ähnlich. $n^k$ bedeutet, dass man die Zahl $n$ $k$-mal mit sich selbst multipliziert, wir berechnen also
$$
\underbrace{n . n \ldots n }_\text{k Faktoren}
$$ Die Produkte, die wir berechnen, haben auch k Faktoren, allerdings ist jeder davon um 1 weniger als der vorhergehende: $$
\underbrace{n . (n-1).(n-2) \ldots (n-k+1) }_\text{k Faktoren}
$$ Diese Produkte haben einen eigenen Namen, sie heißen fallende Faktorielle, oder fallende faktorielle Potenzen. Sie kommen in der Kombinatorik so oft vor, dass es eigene Schreibweisen dafür gibt, nämlich $$ n^\underline{k} \text{ oder } n_{(k)}$$ Die mathematische Definition lautet $$ n^\underline{k} = \prod_{i=0}^{k-1}(n-i)$$ Falls sie diese mathematische Schreibweise nicht gewohnt sind, sollten sie sich davon nicht schrecken lassen. Sie bedeutet nichts anderes als das, was wir schon in Worten ausgedrückt haben. Die oben stehende unterstrichene Zahl (der Exponent) gibt an, wieviele Faktoren das Produkt hat und die unten stehende Zahl ist der erste Faktor; alle weiteren Faktoren werden pro Faktor um 1 verringert.