Wahlwiederholung und statistische Grafiken – ein weiterer Erklärungsversuch

Ich bin einigermaßen verblüfft.

Nämlich über die Reaktionen auf meinen gemeinsam mit Walter Schachermayer verfassten falter-Artikel zur Wahlaufhebung.

Es gibt überraschend viele Leser, die sich weigern unsere Argumentation als schlüssig anzuerkennen.

Insbesondere haben einige Leser Probleme damit, die Wahrscheinlichkeitsaussage

… erhalten wir unter Verwendung anerkannter Modelle und Methoden der Statistik eine Wahrscheinlichkeit von 0,000000000132. Das ist etwa ein Tausendstel der Wahrscheinlichkeit des Lotto-Sechsers.

Es gibt zwar in unserem Artikel einen – wie ich glaube – sehr anschaulichen Vergleich, aber dass es schwierig sein kann, Wahrscheinlichkeitsaussagen sinnvoll einzuordnen, ist eine bekannte Tatsache (und übrigens auch ein Auftrag an die Bildungspolitik).

Ich versuche daher hier noch einmal, eine möglichst einfache und nachvollziehbare Erklärung zu liefern, warum die Daten belegen, dass die Wahl nicht in den 11 vom VfGH beanstandeten Bezirken ergebnisverändernd manipuliert wurde.

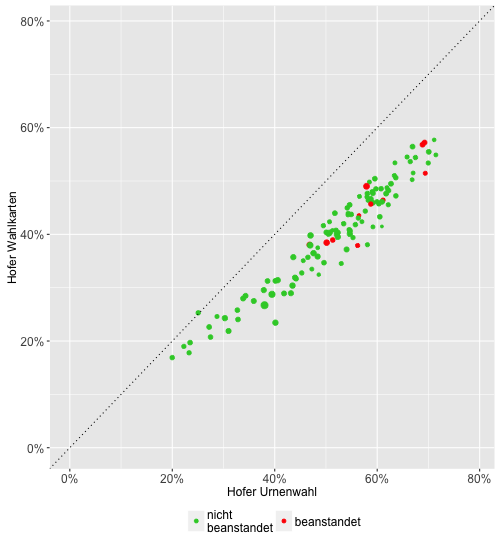
Die folgende Grafik zeigt die Anteile des Kandidaten Hofer in allen 117 politischen Bezirken (und Statutarstädten). Jeder Bezirk wird durch einen Punkt dargestellt. Die x-Koordinate des Punkts (also wie weit der Punkt waagrecht gemessen vom linken Rand entfernt liegt) gibt den Anteil Hofers an den gültigen Urnenstimmen in diesem Bezirk an, die y-Koordinate (also die „Höhe“ des Punkts), den Anteil an den Wahlkartenstimmen in diesem Bezirk.

Alle Punkte bis auf eine Ausnahme liegen unterhalb der strichlierten Diagonalen; das heißt, dass Hofer mit einer einzigen Ausnahme in allen Bezirken bei den Wahlkarten schlechter abgeschnitten hat als bei den Urnenstimmen.

Die Ausnahme ist der Bezirk Wien 4, dort hat Hofer bei den Wahlkarten um 0,3% (also nur geringfügig mehr) besser als bei den Urnenstimmen abgeschnitten.

Die roten Punkte entsprechen den 11 im Erkenntnis des VfGH explizit angeführten Bezirken, bei denen laut VfGH Manipulationen möglich gewesen sind, die grünen Punkte allen anderen Bezirken. Man sieht sofort, dass die roten Punkte genau in das Muster der grünen Punkte passen, sie zeigen keinerlei abweichendes Muster.

Die roten Punkte liegen eher rechts oben, das heißt, dass Hofer in diesen Bezirken besser abgeschnitten hat als in vielen anderen Bezirken, und zwar sowohl, bei den Urnenstimmen als auch den Wahlkartenstimmen.

Wie hätte das Ergebnis in den „roten“ Bezirken aussehen müssen, damit Hofer gewonnen hätte.

Hofer lag im Endergebnis (inklusive Wahlkarten) um 30.863 Stimmen hinter van der Bellen. In den beanstandeten „roten“ Bezirken gab es insgesamt 77.769 gültige Stimmen. Damit Hofer gewinnt hätte er 15.432 (30.863/2 aufgerundet) mehr von diesen Stimmen und van der Bellen 15.432 von diesen Stimmen weniger erhalten müssen. Dann läge Hofer genau eine Stimme vor van der Bellen.

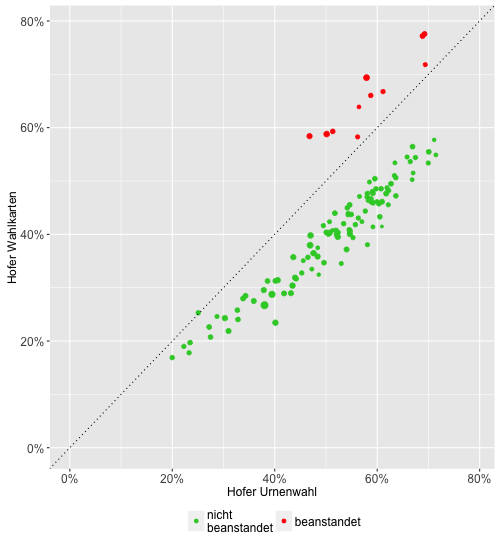
Wenn wir diese 15.432 Stimmen mehr für Hofer anteilsmäßig auf die 11 beanstandeten Bezirke aufteilen und das dann grafisch darstellen ergibt sich folgendes Bild:

Wir sehen sofort, dass Hofer in allen beanstandeten Bezirken bei den Wahlkarten deutlich besser als bei den Urnenstimmem hätte abschneiden müssen. Das wäre ein definitiv anderes Muster als in den nicht beanstandeten Bezirken.

Wenn man Manipulationen unterstellt, dann hätten diese Manipulationen die Punkte von den auffälligen Positionen in der zweiten Grafik (deutlich höher als die grünen Punkte) in die unauffälligen Positionen auf der ersten Grafik (zwischen den grünen Punkten) verschieben müssen.

Man hätte also schon während der Manipulation, *vor* der Auszählung der Wahlkartenstimmen, wissen müssen, wo die grünen Punkte liegen werden. Dazu wären hellseherische Fähigkeiten notwendig gewesen; und zwar für jeden einzelnen der beanstandeten Bezirke. Also entweder Personen mit hellseherischen Fähigkeiten
in jedem dieser Bezirke,
oder eine Verschwörung mit einem zentralen Hellseher, der dann an die Mitglieder der Verschwörung in jedem der 11 Bezirke eine Order über die Zahl der zu manipulierenden Stimmen ausgibt.

Man hätte außerdem im vorhinein wissen müssen, in welchen 11 Bezirken Hofer atypisch besser abschneiden wird als in den anderen Bezirken, um genau dort zu manipulieren.

Schwierig ist dann auch noch die Logistik der Stimmenmanipulation. Man müsste die passende Zahl von Wahlkartenkuverts mit Hofer-Stimmen finden und darin die Hofer-Stimme durch eine van-der-Bellen-Stimme ersetzen.

Wenn man das alles überlegt, dann kann man de facto ausschließen, dass es jemanden gibt, der eine derartige Manipulation zustande bringt.