Wenn jede_r gegen jede_n antreten soll, wieviele Zweierkombinationen gibt es dann?
Heute (14.4.2016) gibts im ORF Diskussionen von je 2 Personen aus 5 Kandidat_inn_en bei der Wahl zum Bundespräsidenten.
Im Vorfeld wurde auf Twitter und auch anderswo diskutiert, warum der ORF Herrn Lugner nicht zu den Zweierdiskussionen eingeladen hat.
Eines der Argumente war, dass man dann – bei 6 möglichen Teilnehmern – 15 Diskussionen machen müsste, und nicht nur 10 wie bei 5 Teilnehmern.
Wie rechnet man aus, wieviele Zweierdiskussionen es bei vorgegebener Anzahl von Teilnehmern gibt?
Das geht ganz einfach.
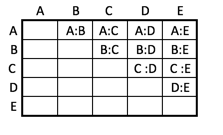
Beginnen wir mit 5 Kandidaten, und nennen wir sie A, B, C, D und E und schreiben wir alle möglichen Zweierdiskussionen in einer Tabelle auf:
Der linke untere Teil dieser Tabelle ist leer weil ja beispielsweise C:A dieselbe Diskussion wäre wie A:C. Wir können auch sagen, dass wir nur Diskussionen zählen, bei der die Diskutanten in alphabetischer Reihenfolge angeführt werden.
Die Anzahl der Diskussionen ist natürlich die Zahl jener Kästchen, in denen eine Paarung steht.
Wieviele das sind können wir auf 2 Arten ermitteln.
Die erste Spalte ist leer, in der 2. Spalte gibt es 1 besetztes Feld, in der 3. Spalte 2 besetzte Felder, in der 4. Spalte 3 und in der 5. Spalte 4 besetzte Felder.
Es gibt also insgesamt 1+2+3+4=10 Zweierdiskussionen.
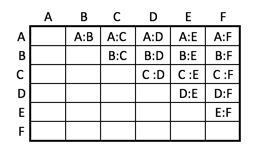
Wenn jetzt ein sechster Kandidat dazukommt, dann schaut die Tabelle so aus:
Es ist also eine 6. Spalte mit 5 Einträgen dazugekommen.
Wenn man weiß, dass es bei 5 Teilnehmern 10 Diskussionen gibt, dann kommen für den 6. Teilnehmer 5 Diskussionen dazu und es gibt daher bei 6 Teilnehmern 15 Diskussionen.
Wir können diese Rechnung auch so aufschreiben.
$$1+2+3+4+5=(1+2+3+4)+5=10+5=15$$
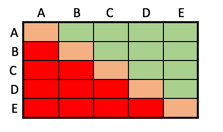
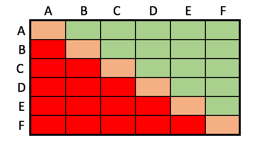
Wir können in den beiden Tabellen auch eine Struktur der (grün markierten) besetzten Zellen erkennen:
Wenn wir die Anzahl der Zeilen und Spalten der beiden Tabellen jeweils mit $n$ bezeichnen, dann hat $n$ bei der kleineren Tabelle den Wert 5 und bei der größeren den Wert 6.
Jede der beiden Tabellen hat dann $n\cdot n=n^2$ Zellen, also $5\cdot 5=25$ bei der kleineren und $6\cdot 6=36$ bei der größeren Tabelle.
Wir müssen die grünen Zellen zählen. Wir nehmen also zuerst die orangen Zellen weg, davon gibts $n$, also 5 oder 6 und es bleiben $n^2-n=n\cdot (n-1)$, also 20 oder 30 Zellen übrig.
Das sind die roten und die grünen Zellen zusammen gezählt.
Wir sehen sofort, dass es in beiden Tabellen genau gleich viele rote und grüne Zellen gibt.
Daher müssen wir nur die Zahl der roten + grünen Zellen halbieren und erhalten dann die Zahl der grünen Zellen. Wir berechnen also $\frac{n\cdot (n-1)}{2}$ für $n=5$ und $n=6$ aus und erhalten $\frac{5\cdot 4}{2}=10$ beziehungsweise $\frac{6\cdot 5}{2}=15$.
Dieses Rezept funktioniert natürlich nicht nur für $n=5$ und $n=6$ sondern für jede beliebige Anzahl $n$.
Wir haben übrigens so ganz nebenbei eine mathematische Formel bewiesen, nämlich
$$1+2+\ldots+(n-1)+n=\frac{n\cdot (n+1)}{2}$$
Wenn man die ganz abstrakte Schreibweise für Summen verwenden will, dann schreibt man
$$\sum_{i=1}^{n}{i}=\frac{n\cdot (n+1)}{2}$$
Davon sollte man sich aber nicht abschrecken lassen, es bedeutet genau dasselbe wie die Formel davor.
(Wenn $n$ die Zahl der Kandidaten ist, dann haben wir eigentlich die Formel $1+2+\ldots+(n-1)=\frac{n\cdot (n-1)}{2}$ bewiesen.)
Wir haben das bewiesen, weil wir die Zahl der grünen Zellen auf zwei verschiedene Arten abgezählt haben und die errechneten Werte daher gleich sein müssen.
Es gibt einen wichtigen Zweig der Mathematik, der sehr oft mit solchen „Abzähltricks“ arbeitet, nämlich die Kombinatorik.
Diese Formel läßt sich auch noch auf eine andere Art beweisen.
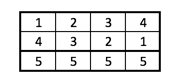
Wir schreiben die Zahlen von 1 bis 4 nebeineinder und direkt darunter die Zahlen von 1 bis 4 in umgekehrter Reihenfolge.
Dann ergibt die Summe zweier übereinander stehender Zahlen immer 5 und die gesamte Summe der oberen beiden Reihen der Tabelle ist $5\cdot 4=20$. Die Summer der zweiten Reihe und der ersten Reihe ist aber gleich und daher ist die Summe der ersten Reihe $\frac{20}{2}=10$.
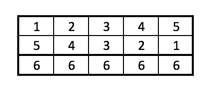
Ebenso ist die Summe der beiden oberen Reihen in dieser Tabelle $6\cdot 5=30$ und daher die Summe der ersten Reihe die Hälfte davon, also $\frac{6\cdot 5}{2}=15$.
Wenn wir die Zahlen von 1 bis 100 addieren wollen, dann geht das natürlich auch nach diesem Rezept und ergibt $\frac{101\cdot 100}{2}=5050$.
Das hat vor ungefähr 230 Jahren schon ein kleiner Volksschüler herausgefunden.
Sein Name war Carl Friedrich Gauss und er wurde später dann einer der berühmtesten und wichtigsten Mathematiker.
Warnung: Diese Erklärungen sind noch nicht zu Ende. Rechnen sie mit einem weiteren Blogeintrag, in dem ich erklären werde, wie man ausrechnet, wieviele Diskussionen es gibt, wenn jede Diskussion 3 oder mehr Teilnehmer haben kann.