Wann gehen wir in Pension und wie lange bleiben wir in Pension
Im profil Nr 7/2012 vom 13. Feber 2010 liest man im Leitartikel Das Amen im Ministerrat folgendes:
Während das Pensionsalter in den vergangenen 40 Jahren um durchschnittlich zwei Jahre gesunken ist, stieg die Lebenserwartung im selben Zeitraum um gut zehn Jahre – macht zwölf Jahre Pension, die nun zusätzlich finanziert werden müssen oder eben nicht.
Im Club 2 vom 8. Feber 2012, 23:00 sagt zum Zeitpunkt 1:15:43 der Sendung der Diskussionsleiter Peter Rabl
Ein Vergleich: 1970 hat ein duchschnittlicher Österreicher 41 Jahre im Beruf verbracht
und war 11 Jahre in Pension, 2012 verbringt er derzeit 38 Jahre im Beruf und ist 23 Jahre in Pension.
Kein Riesenunterschied, aber doch einer. In beiden Fällen lautet die Behauptung, dass die Pensionsdauer im Schnitt um 12 Jahre zugenommen hat. Allerdings ist im ersten Fall ein Sechstel des Zuwachses durch frühere Pensionsantritte verursacht, im zweiten Fall aber ein Viertel des Zuwachses. Der Unterschied ist immerhin so gross, dass es sich lohnt herauszufinden, was nun wirklich stimmt.
Dazu braucht man Daten, und die sind mit ein wenig Mühe im Internet zu finden. Zum Thema Pensionszugangsalter wird man beim Hauptverband der Sozialversicherungsträger fündig. Im Statistischen Handbuch der österreichischen Sozialversicherung findet sich in Kapitel 3 auf Seite 7 eine Tabelle mit dem zeitlichen Verlauf des durchschnittlichen Pensionszugangsalters für alle gesetzlichen Pensionsversicherungen (Beamte sind da aufgrund der völlig anderen Rechtsgrundlage nicht eingeschlossen).
| Männer | Frauen | |
|---|---|---|
| 1970 | 61.9 | 60.4 |
| 2010 | 59.1 | 57.1 |
| Änderung | 2.8 | 3.3 |
Die Durchschnittswerte von Männern und Frauen zeigen, der Pensionsantritt 2010 ziemlich genau um 3 Jahre früher erfolgt als 1970.
Um wieviele Jahre hat die Lebenserwartung zugenommen? Auch dafür findet man Daten im Netz, nämlich die Sterbetafeln von 1947 bis 2010 bei der Statistik Austria.
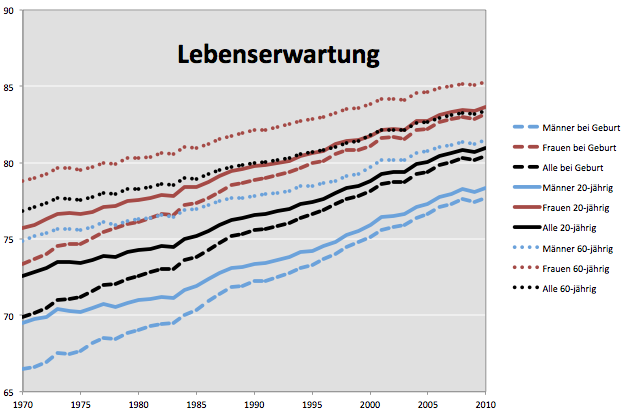
Die Werte der Lebenserwartungen für 1970 und 2010 zeigt die folgende Tabelle:
| Männer | Frauen | Gesamt | |||||||
|---|---|---|---|---|---|---|---|---|---|
| mit 0 | mit 20 | mit 60 | mit 0 | mit 20 | mit 60 | mit 0 | mit 20 | mit 60 | |
| 1970 | 66.5 | 69.5 | 74.9 | 73.4 | 75.7 | 78.8 | 69.9 | 72.6 | 76.8 |
| 2010 | 77.7 | 78.3 | 81.5 | 83.2 | 83.6 | 85.3 | 80.4 | 81.0 | 83.4 |
| Zuwachs | 11.2 | 8.8 | 6.6 | 9.8 | 7.9 | 6.5 | 10.5 | 8.4 | 6.6 |
Die Lebenserwartung bei der Geburt hat also tatsächlich von 1970 auf 2010 um ca. 10 Jahre zugenommen. Zum Teil ist diese Steigerung aber auf die bis etwa 1985 stark sinkende Kindersterblichkeit zurückzuführen und das hat keine unmittelbare Auswirkung auf das Pensionssystem. Im Pensionssystems kommt es auf die Lebenserwartung der Teilnehmer an, also auf die Lebenserwartung aller, die ins Berufsleben eintreten. Daher ist die Lebenserwartung der 20-jährigen relevant für das Pensionssystem. Diese Lebenserwartung hat laut Tabelle um etwa 8.4 Jahre zugenommen. Die Lebenserwartung der 60-jährigen als Grundlage der Berechnungen heranzuziehen wäre irreführend, weil wir dann wieder nur einen Teil der Teilnehmer am System berücksichtigen würden. Will man die Gefahren für das Pensionssystem herunterspielen, dann ist diese Lebenserwartung allerdings besser dazu geeignet als die der 0-jähringen und der 20-jährigem, weil der Zuwachs von 1970 auf 2010 nur 6.6 Jahre beträgt und somit die Verlängerung der Pensionsdauer geringer erscheint.
Jedenfalls kann man auf Grundlage dieser Daten sagen, dass eine vernünftige Beschreibung der Pensionsproblematik davon ausgehen kann, dass im Vergleich zu 1970 die durchschnittliche Pensionsdauer um 11.4 Jahre länger ist und dass 3 Jahre davon auf frühere Pensionsantritte zurückzuführen sind. 3 Jahre sind etwas mehr als ein Viertel von 11.4 Jahren, also ist etwa ein Viertel der Pensionszeitverlängerung auf den früheren Pensionsantritt zurückzuführen.
Wir können mit unseren Daten auch noch weitere Szenarien durchspielen. Wenn wir von einem durchschnittlichen Berufseintrittsalter von 20 Jahren ausgehen, dann war im Jahr 1970 ein Pensionsversicherter 41.1 Jahre aktiv und danach 11.5 Jahre in Pension. Ab Berufseintritt hat er also 78% der Zeit aktiv und 22% der Zeit in Pension verbracht. 2010, bei einem Berufeintrittsalter von 20, einem Pensionsatrittsalter von 58.1 und einer Lebenserwartung von 81.0 betragen die entsprechenden Anteile 63% und 37%. Wenn das Pensionsatrittsalter 2010 statt bei 58.1 bei 67.6 läge, dann wäre der Anteil der aktiven Zeit an der gesamten Lebenserwartung wieder 78% (so wie 1970). Wenn die Lebenserwartung auf 84 steigt, dann ist der Aufteilungsschlüssel 78:22 für das Verhältnis von aktiver Zeit zu Pensionszeit bei einem Pensionsantrittsalter von 70 Jahren erreicht. Ein Pensionsantrittsalter von 75 (wie eben in Norwegen diskutiert wird) ist unter den Rahmenbedingungen von Österreich von 1970 erst bei einer Lebenserwartung von 90.5 Jahren notwendig.
In den letzten 20 Jahren ist die Lebenserwartung der 20-jährigen pro Jahrzehnt um 2.2 Jahre gestiegen. Wenn sich dieser Trend unvermindert fortsetzt, dann würden wir die Lebenserwartung von 84 in etwa 12 Jahren erreichen. Will man also die Aufteilung von aktiver Zeit zu Pensionszeit von 1970 mit der Lebenserwartung von 2025 erreichen, dann ist im Jahr 2025 dazu ein Pensionsantrittsalter von 70 Jahren notwendig.
Alle diese Berechnungen erfordern keine höhere Mathematik, es handelt sich dabei lediglich um etwas kompliziertere Textaufgaben und Schlussrechnungen. Ein wichtiger Aspekt der Analyse ist, dass man sich genau überlegen muss, welche von verschiedenen Kennzahlen, die man berechnen kann, das Problem am besten beschreibt. Weder die Lebenserwartung bei der Geburt noch die Lebenserwartung der 60-jährigen „passt“ als Hauptkennzahl zur Berechnungen zur Pensionsfinanzierung. Sachlich am saubersten ist es, die Lebenserwartung der am System Beteiligten heranzuziehen, und dazu ist die Lebenserwartung der 20-jährigen am ehesten geeignet.
Wünschenswert wäre, wenn schon im Lehrstoff in der Schule derartige Berechnungen vorgesehen wären, denn dann könnten viele Leute selber die Konsequenzen verschiedener Massnahmen zur Pensionssicherung überprüfen.
Ich habe vor ca. 15 Jahren in einer Fortbildungsveranstaltung für Mathematik-Lehrer ein derartiges Projekt bearbeitet. Ein erheblicher Teil dieser Mathematik-Lehrer hat mir in der Nachbesprechung dann gesagt, dass derartige Beispiel im Mathematikunterricht nichts verloren hätten, weil es sich ja um ganz konkrete und reale Zahlen handele und derartiges im Mathematikunterricht wohl keinen Platz habe.
Bei den PISA-Aufgaben gibt es einen Block von Mathematik-Aufgaben, der sich mit der Interpretation von Bevölkerungspyramiden beschäftigt. Bei diesen Aufgaben schneidet Österreich im Vergleich mit anderen Ländern besonders schlecht ab.
Vielleicht hat die Tatsache, dass in der öffentlich stattfindenden Pensionsdiskussion immer noch zu wenig über die zahlenmässigen Konsequenzen verschiedener möglicher Tatsachen diskutiert wird, auch mit der beschriebenen Einstellung mancher Mathematiklehrer und dem daraus resultierenden Mangel an Kenntnissen zu einfachen Berechnungen zur Pensionsproblematik zu tun.
2 Comments
Leider werden in solchen Berechnungen die Produktivitätszuwächse nicht berücksichtigt, die nur in geringem Ausmaß über die Löhne weitergegeben werden. Daher sollten wir über Modelle àla Wertschöpfungsabgabe zur Sicherung der Pensionen diskutieren.
Es wäre schön, wenn die öffentlich auftretenden Pensionsexperten die Grundlagen ihrer Modelle ebenso klar darstellen würden.
Noch eine Anmerkung zum Vergleich.
Man müsste auch sicherstellen, dass die Erfassung vergleichbare Definitionen verwendet. Im Club 2 war auch von Invaliditätspensionen die Rede, welche das Antrittsalter deutlich senken, auch im Vergleich zum Ausland. Darauf wurde aber dann nicht mehr Bezug genommen.