Don’t-Smoke-Volksbegehren und NRW 2017
Auf addendum.org gibt es eine sehr aufschlussreiche Analyse des Zusammenhangs von Don’t-Smoke-Volksbegehren und Nationalratswahl 2017.
Ich habe dazu noch eine weitere Analyse gemacht. In meiner Analyse kann man die Unterschiede zwischen den Bundesländern etwas genauer sehen.
Das Kärntner Wahlrecht und seine seltsamen Folgen
Bei der Kärntner Landtagswahlordnung kann passieren, dass eine Partei mit mehr Stimmen weniger Mandate bekommt. Ich habe ein paar solcher Effekte in einem Artikel im standard zusammengestellt.
Eine Excel-Arbeitsmappe zum Durchrechnen verschiedener Szenarien gibts auch (zum Download).
Warum das Skalarprodukt doch nicht ganz überflüssig ist.
Armin Wolf schreibt in seinem neu eingerichteten lesenswerten Blog darüber, warum der Oberstufen-Mathematikunterricht in seiner gegenwärtigen Form seiner Meinung nach falsch läuft. Eins seiner Beispiele lautet:
„Beachte: Das skalare Produkt zweier Vektoren ist kein Vektor, sondern eine reelle Zahl.“ Das steht im „Kompendium zur Maturavorbereitung“ eines aktuellen Mathe-Schulbuchs. Stimmt ganz sicher, aber wozu muss ein Maturant das nochmal unbedingt wissen?
Es gibt ein paar Gründe, das zu wissen. Und wenn der Unterricht diese Gründe nicht vermittelt, dann ist eben das das Problem, aber nicht die Tatsache an sich.
Das skalare Produkt ist ganz einfach erklärt. Man sieht es auf jeder Billa-, Merkur- oder Hofer-Rechnung: da werden für jeden Posten Mengen mit Preisen pro Einheit multipliziert und diese Gesamtpreise pro Posten addiert, und das ergibt die Gesamtsumme.
Man hat also zwei gleiche lange Zahlenkolonnen, und man multipliziert die beiden ersten Zahlen miteinander, und die beiden zweiten Zahlen, und die beiden dritte Zahlen und so weiter, und diese Produkte addiert man dann. Diese Summe ist das skalare Produkt. In Tabellenkalkulationsprogrammen (z.B. in Microsoft Excel) gibts die Funktion SUMMENPRODUKT (in der englischen Version SUMPRODUCT), die macht genau das.
Zahlenkolonnen sind Vektoren, und daher kann man sagen, dass der Gesamtpreis das skalare Produkt des Preisvektors mit dem Mengenvektor ist.
Indices (z.B. der Index der Verbraucherpreise) sind auch Produkte von Mengen mit Preisen, man kann sie mathematisch also auch als inneres Produkt verstehen.
Das skalare Produkt kommt in „anderen mathematischen Gegenden“ vor. Vektoren sind ja auch etwas geometrisches. Koordinaten sind klassischer Schulstoff, und Koordinatenvektoren sind dann eben die zusammengefassten Koordinaten. 2-dimensionale und 3-dimensionale Vektoren entsprechen dabei Punkten in der Ebene oder im Raum.
Ich gehe jetzt einmal davon aus, dass außer Streit steht, dass Geometrie und Koordinatengeometrie wesentliche Bildungsinhalte sind, die man nicht aus dem Curriculum streichen sollte.
Jetzt wirds ein bisschen „technischer“, weil man das, was kommt, nicht ganz ohne Formeln aufschreiben kann.
Eine wichtige geometrische Operation ist es, Winkel zwischen Vektoren zu berechnen. Oft stellt sich auch die Frage, ob zwei Vektoren einen rechten Winkel bilden (z.B. auf einem Wohnungsplan). Und da gibts ein sehr einfaches Hilfsmittel: Zwei Vektoren (können Zimmerwände beschreiben) bilden dann einen rechten Winkel, wenn ihr skalares Produkt den Wert 0 hat. Das können ganz beliebige Vektoren sein, sie müssen nicht parallel zu den Koordinatenachsen sein. Und das gilt auf gleiche Weise im 2-dimensionalen wie im 3-dimensionalen! Das innere Produkt hat also Eigenschaften, die in verschiedenen Geometrien (eben und räumlich) gleichartig funktionieren. Nicht sofort zu erwartende Analogien in verschiedenen Zusammenhängen zu entdecken und herauszuarbeiten ist eine der wesentlichsten Methoden der Mathematik.
In der Mathematik schreibt man das dann so auf:
Wenn $x=(x_1,x_2,…x_n)$ und $y=(y_1,y_2,…y_n)$ zwei Vektoren gleicher Länge $n$ sind, dann ist
$$ x.y=\sum_{i=1}^{n}x_i y_i $$
das innere innere Produkt dieser beiden Vektoren.
Wenn $n=2$ ist, wir also Geometrie in der Ebene betreiben, dann wird daraus
$$x.y=x_1\cdot y_1 + x_2\cdot y_2$$
Betreibt man räumliche Geometrie, dann ist $n=3$ und die Formel lautet
$$x.y=x_1\cdot y_1 + x_2\cdot y_2 + x_3\cdot y_3$$
Diese Formeln wirkt vielleicht auf manche Leser(innen)? etwas abschreckend, sie aber bedeutet nichts anderes als das, was wir oben besprochen haben: wir multiplizieren die einander entsprechenden $x$e und die $y$s miteinander und addieren alle diese Produkte. Die Formel ist nur die mathematische Kurzschrift dafür.
Das skalare Produkt ist in der Geometrie aber noch weitaus ergiebiger:
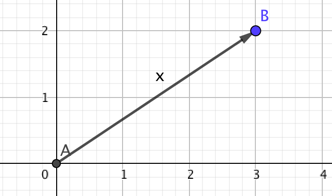
Wie berechnet man die Länge einer Strecke beziehungsweise eines Vektors:
Der Abstand der Punkte in x-Richtung ist 3, in y=Richtung 2. Daher ist der Abstand insgesamt $\sqrt{3^2+2^2}=\sqrt{13}$
Unter dem Wurzelzeichen steht $3\cdot 3 + 2 \cdot 2$, also das innere Produkt $(3,2).(3,2)$. Man sagt dann auch das ist das innere Produkt des Vektors $x$ mit sich selbst.
Anmerkung: Das Produkt eines Objekts mit sich selbst ist in der Mathematik nichts Außergewöhnliches; das Quadrat einer Zahl ist das Produkt einer Zahl mit sich selbst.
Das skalare Produkt eines Vektors mit sich selbst ist also das Quadrat seiner Länge. Wieder tritt das skalare Produkt in einem neuen Kontext auf.
Die mathematische Kurzschrift dafür geht so ($|x|$ bezeichnet die Länge eines Vektors x):
$$|x|^2=x.x$$
Es kann aber noch mehr.
Wenn wir den Winkel zwischen den Strecken (oder Vektoren) $AB$ und $AC$ berechnen wollen, dann gilt für diesen Winkel $\alpha$
$$ \cos(\alpha ) = \frac{x.y}{|x||y|}$$
Das schaut jetzt schon etwas komplizierter aus. Was bedeutet es.
Auf der rechten Seite der Gleichung stehen 3 skalare Produkte, 2 davon sind aber Längen, also skalare Produkte von Vektoren mit sich selber.
Will man den Winkel finden, dann braucht man (abgesehen von einigen Ausnahmefällen) eine Tabelle oder einen Taschenrechner oder Computer.
In unserem Fall haben wir daher
$$\cos(\alpha)=\frac{3\cdot 1+2 \cdot 3}{\sqrt{2^2+3^2}\sqrt{1^2+3^2}}
=\frac{9}{\sqrt{13}\sqrt{10}}=\frac{9}{\sqrt{130}}$$
Numerisch berechnet ergibt das $\cos(\alpha)=0.7893$ und $\alpha=37.87^{\circ}$
Das skalare Produkt ist jedenfalls eine Rechenoperation, die in der Mathematik in einigen Gebieten vorkommt, bei denen man nicht gleich sieht, dass es analoge Strukturen gibt. Deswegen verdient es einen eigenen Namen und eine Analyse seiner Eigenschaften.
Es heißt auch inneres Produkt.
Wenn in der Mathematik von einem Produkt die Rede ist, dann wird in der Regel aus 2 Objekten ein drittes, gleichartiges Objekt erzeugt. Das Produkt zweier ganzer Zahlen ist eine ganze Zahl, das Produkt zweier Brüche ist wieder ein Bruch usw. Beim skalaren Produkt wird aber aus 2 Vektoren (also Zahlenkolonnen) eine einzige Zahl erzeugt. Die Merkregel, die Armin Wolf moniert, ist eine Erinnerungshilfe. Eigentlich sollte man sie gar nicht brauchen, denn wenn man mit Vektoren hantiert, dann verwendet man das Wort „Skalar“, wenn man nur von einer Zahl und nicht von einem Vektor (der aus mehreren Zahlen besteht) spricht.
Der Name „skalares Produkt“ selbst ist also schon ein sehr deutlicher Hinweis darauf, dass das Ergebnis einer Rechenoperation nicht von der gleichen Art wie die Inputs ist.
Das Problem der Schule besteht möglicherweise darin, dass solche Zusammenhänge nicht klar genug herausgearbeitet werden und daher statt Verständnis für Zusammenhänge eher das Auswendiglernen einzelner Bezeichnungen und Formeln gefördert und geprüft wird.
Das skalare Produkt spielt nicht nur als „Rechenmerkregel“ und in der Geometrie eine Rolle, in vielen statistische Verfahren kommen Rechenschritte vor, die man am einfachsten als skalares Produkt anschreiben kann. Und in der Quantenphysik spielt das skalare Produkt in vielen Formeln ebenfalls eine wichtige Rolle.
Es gibt übrigens auch ein anderes Produkt zweier Vektoren, das heißt Vektorprodukt oder Kreuzprodukt.
Aber das ist eine andere Geschichte.
Wählerstromanalyse Landtagswahl Niederösterreich 2018
Meine Wählerstromanalyse, die ich für ServusTV durchgeführt habe, kann man jetzt in verschiedenen Formen konsumieren.
Ein seltsames Schachproblem
Unter meinen regelmäßig erscheinenden mathematischen Puzzles (#mathepuzzle von @neuwirthe auf Twitter) ist auch folgendes:
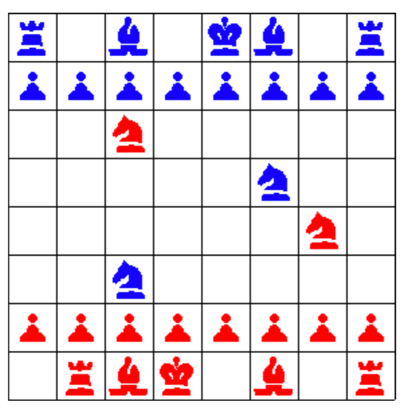
Auf dem abgebildeten Schachbrett gibt es rote und blaue Figuren.
Welche davon wären auf einem regulären Schachbrett und in einer korrekt nach den Schachregeln abgelaufenen Partie weiß und welche schwarz?
Wenn ihnen die Frage seltsam vorkommt, dann haben sie wahrscheinlich recht.
Es gibt aber tatsächlich eine eindeutige Lösung. Um sie zu finden muss man nicht gut Schach spielen können, sondern nur die Regeln kennen.
Wenn sie meinen, dass die Spieler keine besonders guten Spieler sind, haben sie ebenfalls recht. Die Stellung im Spiel wurde aber durch eine Folge regelkonformer Züge erreicht.
Wenn sie weiter scrollen, dann kommen sie zur Auflösung.
Relativ schnell sieht man, dass der blaue Springer in der 3. Reihe von unten dem roten König Schach gibt. Er muss also die letzte gezogene Figur sein. Was muss man noch wissen, damit man entscheiden kann ob er„logisch“ weiß oder schwarz ist?
Weiß hat immer den ersten (Halb-)Zug. In klassischer Schachsprechweise ist ein Zug nämlich immer die Bewegung einer weißen und danach einer schwarzen Figur, die Bewegung nur einer Figur heißt Halbzug.
Wenn wir die Halbzüge durchnummerieren, dann ist jeder ungerade Halbzug ein weißer und jeder gerade ein schwarzer Halbzug. Wenn wir also herausfinden, dass es insgesamt ungerade viele Halbzüge gegeben hat, dann wissen wir, dass die zuletzt gezogene Figur weiß war, und wenn die Zahl der Halbzüge gerade war, dann ist die letzte gezogene Figut eine schwarze.
Als allererstes stellen wir fest, dass die Bauern noch nicht bewegt wurden, denn sie können nicht verlustfrei Platz tauschen.
Danach fangen wir mit den blauen Türmen rechts und links oben an.
Beide stehen am ursprünglichen Aufstellungsort. Sie könnten sich jeweils um ein Feld nach innen und dann wieder nach außen bewegt haben, und das sogar mehrfach, die Anzahl der Halbzüge insgesamt ist da gerade.
Die roten Türme können sich auch jeweils nur um ein Feld seitlich bewegt haben. Der Turm links unten steht nicht auf seinem ursprünglichen Feld, er muss also eine ungerade Zahl von Halbzügen oft bewegt worden sein, der rechte muss (analog zu den roten) gerade oft bewegt worden sein. Insgesamt sind die Türme also ungerade oft bewegt worden.
Die Könige können sich (wie die Türme) ebenfalls nur ein Feld zur Seite bewegen. In der Startaufstellung steht der weiße König links von der weißen Dame, der schwarze König rechts von der schwarzen Dame. Sie stehen auf jeden Fall in derselben Spalte des Schacbretts. In unserer Stellung stehen sie in verschiedenen Spalten. Wir wissen nicht, welcher von beiden in der „falschen“ Spalte steht, aber der in der falschen Spalte muss ungerade oft gezogen worden sein, und der andere gerade oft. Beide zusammen müssen also ungerade oft gezogen worden sein.
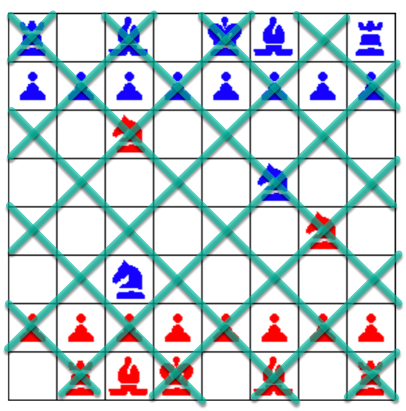
Jetzt noch zu den Springern. Da hilft folgende Überlegung: Die Felder auf dem Schachbrett sind ja in einenm Diagonalmuster in zwei verschiedene Farben eingefärbt. Hier das Muster:
Springer der gleichen Farbe stehen zu Spielbeginn auf Feldern verschiedener Farbe, und jeder Springer wechselt bei jedem Halbzug von einem Feld einer Farbe zu einem Feld der anderen Farbe.
In unserer Problemstellung stehen die blauen Springer auf Feldern verschiedener Farbe, wurden also zusammen gerade oft bewegt. Die roten Springer stehen auf Feldern gleicher Farbe und wurden daher ungerade oft bewegt. Alle 4 Springer wurden zusammen also ungerade oft bewegt. Andere Figuren konnten nicht bewegt werden.
Die Bilanz aller Halbzüge lautet also: Türme ungerade, Könige ungerade, Springer ungerade. Insgsamt also ungerade viele Halbzüge.
Daher ist die letzte gezogene Figur, der blaue Springer in der 3. Reihe von unten, „logisch“ eine weiße Figur.
Hier noch ein paar Tweets, die zu dieser Aufgabe eingelangt sind:
In jedem ordentlichen Schachkaffee bekommt man für sowas auf Lebenszeit Lokalverbot… 😉
Beide Damen von Pferden gefressen, ohne dass die Bauern sich bewegt haette? Wie soll denn das zustande gekommen sein?
Himmel! Ich bin ein so schlechter Schachspieler, dass ich die Startaufstellung googlen musste. Die ist nicht rotationssymmetrisch. Dann ist rot schwarz.
Besonders gefreut hat mich das:
Und jetzt, wo es spannend wird, muss ich zum Einkauf! Wartet ihr bitte auf mich? 😉