Warum Statistiker nach Wahlen leiden müssen

Nach jeder Wahl wird analysiert, welche Wählergruppe sich wie auf die Parteien verteilt hat. Auch nach der Landtagswahl 2013 in Tirol ist das so.

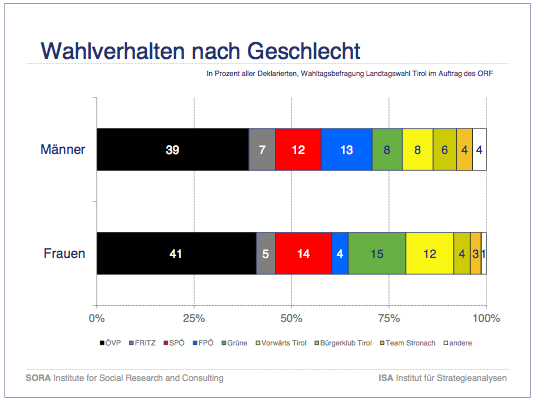
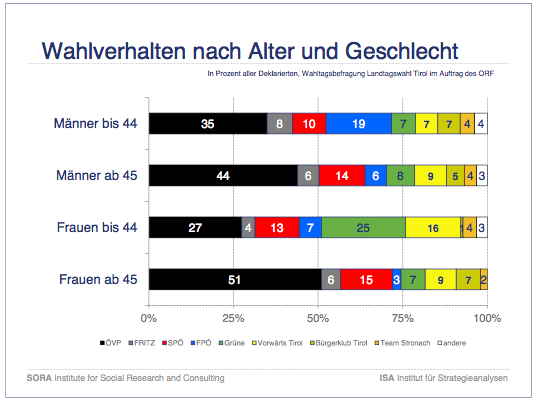
Hier 2 Beispiele solcher Analysen:

Diese Grafiken finden sich in der Wahlanalyse von ISA und SORA

Die zweite Analyse wird auf der Facebook-Seite von Christoph Chorherr heftig diskutiert.

Einem Statistiker fällt auf, daß bei keiner der beiden Grafiken die statistische Schwankungsbreite der Parteienanteile angegeben wird. In der ISA-SORA-Analyse findet man einige Zahlen zu dieser Fragestellung; allerdings findet man leider nicht alle Zahlen, die man braucht, um die Schwankungsbreite der Anteile in den obigen beiden Grafiken ausrechnen zu können.

Mit etwas Detektivarbeit kann man allerdings die Schwankungsbreiten doch annähernd berechnen.
Die Anzahl der Befragten ist n=1227. Laut Angaben wurden die Daten nach Geschlecht, Alter, Bildung und Erwerb gewichtet, die zu einer Überprüfung notwendigen Zahlen stehen aber nicht öffentlich zur Verfügung. Zur Abschätzung der Schwankungsbreiten kann man aber zunächst einmal auch diese Schwankungsbreiten für ungewichtete Schätzwerte berechnen.

n=1227 ergibt eine Schwankungsbreite von maximal 2,8% für geschätzte Anteile an der Grundgesamtheit aller Wahlberechtigten, und diese Zahl findet man auch in der zitierten Quelle. In den Analysen unserer Grafiken geht es aber um Anteile an Männern, Frauen, und auch noch nach Altersgruppen unterteilten Gruppen von Männern und Frauen. In diesen Grafiken werden außerdem nur Anteile an deklarierten Wähler ausgewiesen, also ist die Grundgesamtheit in diesem Fall die Grupper der deklarierten Wähler. Bei eine Wahlbeteiligung von weniger als 60 Prozent ist also für diese Untersuchungen die Stichprobengröße etwa 700. Sollte es außer den Nichtwählern auch Befragte gegeben haben, die zwar gewählt, sich bei der Umfrage aber nicht deklariert haben, dann kann die relevante Stichprobengröße auch nur 550 betragen. Dabei nehmen wir eine Nichtdeklarationsquote von 20% der Wähler an, was laut Auskunft von Meinungsforschern durchaus immer wieder vorkommt.

Gehen wir nun bei unseren weiteren Rechnungen von einer Stichprobengröße 600 für die deklarierten Wähler aus.

Etwa die Hälfte der Wähler sind jeweils Männer und Frauen (das stimmt zwar nicht genau, ist aber genau genug für die Berechnungen der Schwankungsbreiten).
Wenn wir also die Schwankungsbreiten der Parteienanteile bei Männern und Frauen berechnen, dann ergibt sich 5,8%. Damit man davon reden könne, dass der Anteil der ÖVP bei den Männern signifikant verschieden vom Anteil bei den Frauen ist müsste die Differenz in der Stichprobe sogar 8,2% betragen. Nach solchen Berechnungen stellen sich die Geschlechterdifferenzen nur bei den Grünen und bei der FPÖ als signifikant heraus.

Noch größer sind die statistischen Schwankungsbreiten bei der Einteilung nach Geschlecht und Alter. Die 4 untersuchten Gruppen sind annähernd gleich groß. Genau genommen ist die Gruppe der Frauen über 44 etwas größer als die 3 anderen Gruppen, aber der Unterschied ist so klein, dass wir ihn für unsere Berechnungen außer acht lassen können.

Bei 600 deklarierten Wählern ist also jede der 4 Teilgruppen etwa 150 Wähler groß.
Die statistische Schwankungsbreite ist dann maximal 8,1%. Die maximale Schwankungsbreite für einen Anteilsunterschied in 2 Gruppen ist dann 11,5%. Der Unterschied der ÖVP-Anteile zwischen älteren und jüngeren Männern beträgt 9%, ist also statistisch nicht signifikant und sollte daher nicht als politisch relevant interpretiert werden. Der entsprechende Unterschied zwischen den älteren und den jüngeren Frauen ist größer 11,5%, er ist also statistisch signifikant und politisch relevant.
Etwas vergröbernd kann man sagen, dass ganz generell die Unterschiede zwischen älteren und jüngeren Frauen statistisch signifikant sind, entsprechendes für die Männer aber nicht gilt.

Ganz wichtig ist folgendes:
In den untersuchten (und vielen ähnlichen) Grafiken steckt hinter jedem der aufgeteilten Balken eine andere Stichprobe mit jeweils anderer Anzahl von Befragten. Die Schwankungsbreite der geschätzten Anteile kann man nur berechnen, wenn man die Stichprobengröße kennt. Daher wäre es ein Gebot der Sauberkeit, diese Zahl auch bei jedem „Aufteilungsbalken“ anzugeben.

Wenn diese Zahlen aber fehlen, dann kann bei statistisch nicht ganz fachkundigen Lesern der Eindruck entstehen, dass die Größe der gesamten Stichprobe (n=1227) auch die Schwankungsbreite der Parteienanteile in Untergruppen bestimmt. Das ist aber, wie wir gesehen haben, definitiv nicht der Fall.

Lange Zeit wurden bei Meinungsumfragen nicht einmal die Gesamtstichprobengrößen ausgewiesen. Wir Statistiker haben uns das immer gewünscht. Dieser Wunsch wird uns in letzter Zeit auch schon erfüllt.

Jetzt erweitern wir die Wunschliste: Wenn es um Parteienanteile in Untergruppen der Wahlberechtigen geht (z.B. Altersgruppen), dann wüssten wir auch gerne die Stichprobengrößen für diese Untergruppen.
Erst so können politisch interessierte Leser die Zuverlässigkeit von Aussagen über Untergruppen halbwegs abschätzen.

Und noch einen inhaltlichen Wunsch habe ich. Die Nichtwähler waren bei dieser Wahl schon die größte Wählergruppe. Eine Aufgliederung des Nichtwähleranteils nach Alter und Geschlecht wäre meiner Meinung nach eine der interessantesten Analyse nach dieser Wahl. Leider ist die bei den Analysen von ISA-SORA nicht dabei.

Schlagwörter: Statistik, Wahlen

Was kann man aus Meinungsumfragen erschließen und was nicht?

Im Jahr 2013 kommen einige Wahlen und Volksbefragungen auf uns zu.

Im Jänner die Volksbefragung zur Wehrpflicht, spätestens im Oktober die Nationalratswahl, und vorher schon Landtagswahlen in Kärnten, Niederösterreich und Tirol.
In Deutschland gibt’s Landtagswahlen in Niedersachsen, Bayern und Hessen und im September die Bundestagswahl.

Daher liest und hört man immer wieder die Ergebnisse und Interpretationen von Meinungsumfragen. Für einen Statistiker bedeutet das einen ziemliche hohen Leidensdruck, weil sehr oft aus Meinungsumfragen Dinge herausgelesen werden, die auch bei nachsichtigstem Umgang mit den Interpretatoren (in der Regel Journalisten und Politikern) jeder vernünftigen statistischen Grundlage entbehren.

Mit der folgenden Tabelle kann man 2 methodische Fragen beantworten:

1. Wie groß ist die Schwankungsbreite für den Anteil einer Partei bei allen Wahlberechtigten, wenn er in  einer Stichprobe erhoben wurde?
2. Kann man aufgrund einer Stichprobe sagen, dass eine Partei derzeit einen höheren Anteil an allen Wahlberechtigten hat als eine andere Partei?

Sie können diese Excel-Tabelle auch auf ihren Rechner laden. Dazu müssen sie nur auf das Excel-Symbol in der schwarzen Leiste unterhalb der Tabelle klicken.

Wenn sie die Seite in ihrem Browser neu laden, dann sehen sie wieder die Tabelle mit den ursprünglichen Werten.

Einige Zahlenspielereien

Typischerweise geben nicht alle Befragten eine auswertbare Antwort. Wie wirkt es sich denn aus, wenn nur 80% der Befragten eine auswertbare Antwort geben? Dann werden alle Schwankungsbreiten größer, und etwas vereinfacht gesagt werden dann alle Schwankungsbreiten mit 1,1 multipliziert. Liegt der Anteil bei 70%, dann werden die Schwankungsbreiten ungefähr mit 1,15 multipliziert. Sie können das in der Tabelle ausprobieren.

Noch etwas kann man in der Tabelle nachrechnen: wenn man den Umfang der Stichprobe vergrößert und dazu verdoppelt, dann wird die Schwankungsbreite nicht halb so groß, sondern etwa 70% so gross. Erst wenn man die Stichprobe 4x so groß wie ursprünglich macht, dann wird die Schwankungsbreite halbiert. Die genauen Formeln finden sie im nächsten Abschnitt.

Die Tabelle illustriert eine weitere wichtige Tatsache: beim Vergleich der Anteile von zwei Parteien kann man nicht die Formel für die Schwankungsbreite für eine Partei verwenden. Folgender Schluss ist falsch:

Partei A hat in der Stichprobe 25,4%, und die Schwankungsbreite beträgt 2,7%. Partei B hat 22,4%. Dieser Anteil (22,4%) liegt außerhalb des „Sicherheitsbereichs“ (22,7% bis 28,1%) vom Partei A und daher kann man mit ausreichender Sicherheit sagen, dass Partei A auch bei allen Wahlberechtigten vor Partei B liegt.

Mann muss für den Schwankungsbereich der Parteiendifferenz eine eigene Formel verwenden, und in unserem Beispiel ergeben die Berechnungen, dass das Intervall für den Unterschied von -1,3% bis 7,3% geht. Es enthält also sowohl positive als auch negative Werte, und daher kann man nicht sagen, dass eine der beiden Parteien vor der anderen liegt.

In vielen Tageszeitungen findet man Interpretationen von Meinungsumfragen, die die Schwankungsbereiche überhaupt nicht berücksichtigen. Die Situation bessert sich, Qualitätszeitungen weisen mittlerweile schon öfter auf Schwankungsbreiten hin.
Die Schwankungsbreiten für Parteiendifferenzen werden aber kaum je verwendet. In der Folge wird oft davon gesagt oder geschrieben, dass eine Partei vor der anderen läge. Das stimmt dann meist in der Stichprobe; für die Grundgesamtheit aller Wahlberechtigten kann man das aber meist nicht mit ausreichender Sicherheit sagen.

Ein kleines Beispiel: Hat man 2 Parteien, die sich im Bereich vom 20% bis 25% bewegen, dann kann man erst dann sagen, dass eine Partei vor der anderen liegt, wenn der Unterschied in der Stichprobe mindestens 4,4% beträgt

Noch eine Anmerkung: Die Tabelle kann man sinnvollerweise erst bei Stichprobengrößen von mehreren hundert Befragten anwenden.

Für welche Art von Stichproben funktioniert das?

Die Tabelle und die Formeln im nächsten Abschnitt gehen davon aus, dass die Auswahl der Befragten per Zufallsstichprobe erfolgt.

Man sollte also ein Verzeichnis aller Wähler haben und dann mit einem Zufallsmechanismus (meist sind das computergenerierte Zufallszahlen) die zu Befragenden aus dieser Liste auswählen. Dieses Ideal ist sicher schwer zu erfüllen. Die entsprechenden Voraussetzungen werden sicher dann nicht eingehalten, wenn die einzelnen Interviewer selber die zu Befragenden bestimmen können, wie das bei manchen Varianten des Quotenverfahrens der Fall ist.

Ein weit verbreitetes Missverständnis besteht darin, zu glauben, dass die Repräsentativität der Stichprobe das zentrale Qualitätskriterium wäre. Das entscheidende Kriterium dafür, dass unsere Tabelle und unsere Formeln die gewünschte Treffsicherheit haben, ist die Zufallsauswahl. Eine korrekt durchgeführte Zufallsauswahl liefert Repräsentativität als Nebeneffekt.

Die Formeln

Jetzt geht’s ans Eingemachte. Wenn sie sich mit Formeln nicht sehr wohl fühlen, dann müssen sie diesen Abschnitt nicht mehr lesen. Sie können die Tabelle weiter oben auch so verwenden, wenn sie die Erläuterungen zur Tabelle berücksichtigen.

Die Basisformel für Umfragegenauigkeit lautet:
Wenn wir in einer Umfrage mit $n$ Befragten in der Stichprobe eine Anteil von $\hat{p}$ erhalten, dann berechnet man die Schwankungsbreite für die Sicherheit $\alpha$ als
$$d=z_{\alpha}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$$ und der Bereich, in dem der entsprechende (unbekannte) Anteil an der Grundgesamtheit liegt, lautet $$\hat{p}\pm d$$

$z_{\alpha}$ ist ein Wert, den man in Normalverteilungstabellen nachschlagen kann. Der meist verwendete Wert ist $z_{0,95}=1,96$.
Das ergibt sich aus dem Anspruch, in 19 von 20 Fällen (also in 95% aller Fälle) eine korrekte Aussage zu machen. Stellt man höhere Sicherheitsansprüche, dann verwendet man $z_{0,99}=2,58$. Dann sind die statistischen Schlussfolgerungen in 99 von 100 Fällen korrekt.

Excel kann die Werte $z_{\alpha}$ ebenfalls berechnen.

Die statistisch-mathematisch korrekte Formulierung, die die Grundlage von Anteilsberechnungen bei Meinungsumfragen liefert, lautet:

Wenn der Anteil eines bestimmten Merkmals in einer Zufallsstichprobe vom Umfang $n$ den Wert $\hat{p}$ hat, dann liegt der entsprechende Anteil in der Grundgesamtheit mit Sicherheit $\alpha$ zwischen den Werten $\hat{p}-z_{\alpha}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$ und $\hat{p}+z_{\alpha}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$

Wenn wir die Anteile zweier Parteien in einer Stichprobe schätzen, dann lautet die statistisch korrekte Formulierung samt Formel:

Wenn die Anteile zweier einander ausschließender Merkmale in einer Zufallsstichprobe vom Umfang $n$ die Werte $\hat{p}_A$ und $\hat{p}_B$ und die Anteilsdifferenz daher die Werte $\hat{p}_A-\hat{p}_B$ haben, dann liegt die entsprechende Anteilsdifferenz in der Grundgesamtheit mit Sicherheit $\alpha$ zwischen den Werten $\hat{p}_A-\hat{p}_B-z_{\alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B-(\hat{p}_A-\hat{p}_B)^2}{n}}$ und $\hat{p}_A-\hat{p}_B+z_{\alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B-(\hat{p}_A-\hat{p}_B)^2}{n}}$

Schlagwörter: Statistik, Wahlen