Wählerstromanalyse und Wahlhochrechnung
Die Folien zu meinem Vortrag, in dem ich die statistische Methodik von Wählerstromanalyse und Wahlhochrechnung (hoffentlich auch für Nichtfachleute verständlich) erkläre, gibt es hier:
http://www.wahlhochrechnung.at/vortrag/
Ich hab den Vortrag am 11. Mai 2016 an der Universität Wien gehalten, wiederhole das aber gerne, wenn ich eingeladen werde 😉
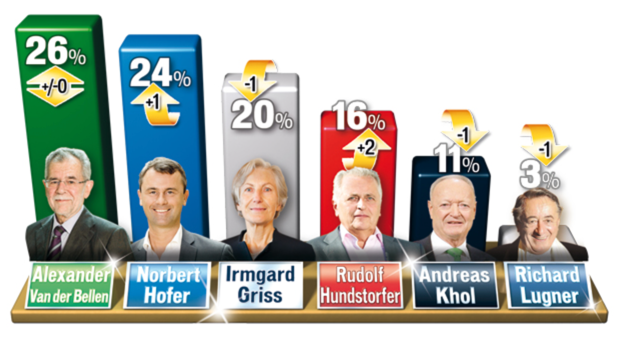
Wahlhochrechnung zur Bundespräsidentenwahl
Am 24. April (und voraussichtlich auch am 22. Mai) werde ich wieder hochrechnen.
Die Hochrechnung gibts ab 17 Uhr auf www.wahlhochrechnung.at.
Wenn jede_r gegen jede_n antreten soll, wieviele Zweierkombinationen gibt es dann?
Heute (14.4.2016) gibts im ORF Diskussionen von je 2 Personen aus 5 Kandidat_inn_en bei der Wahl zum Bundespräsidenten.
Im Vorfeld wurde auf Twitter und auch anderswo diskutiert, warum der ORF Herrn Lugner nicht zu den Zweierdiskussionen eingeladen hat.
Eines der Argumente war, dass man dann – bei 6 möglichen Teilnehmern – 15 Diskussionen machen müsste, und nicht nur 10 wie bei 5 Teilnehmern.
Wie rechnet man aus, wieviele Zweierdiskussionen es bei vorgegebener Anzahl von Teilnehmern gibt?
Das geht ganz einfach.
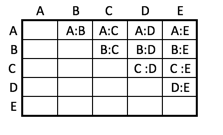
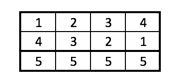
Beginnen wir mit 5 Kandidaten, und nennen wir sie A, B, C, D und E und schreiben wir alle möglichen Zweierdiskussionen in einer Tabelle auf:
Der linke untere Teil dieser Tabelle ist leer weil ja beispielsweise C:A dieselbe Diskussion wäre wie A:C. Wir können auch sagen, dass wir nur Diskussionen zählen, bei der die Diskutanten in alphabetischer Reihenfolge angeführt werden.
Die Anzahl der Diskussionen ist natürlich die Zahl jener Kästchen, in denen eine Paarung steht.
Wieviele das sind können wir auf 2 Arten ermitteln.
Die erste Spalte ist leer, in der 2. Spalte gibt es 1 besetztes Feld, in der 3. Spalte 2 besetzte Felder, in der 4. Spalte 3 und in der 5. Spalte 4 besetzte Felder.
Es gibt also insgesamt 1+2+3+4=10 Zweierdiskussionen.
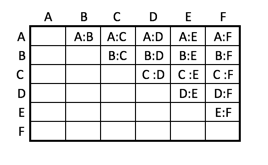
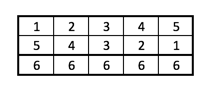
Wenn jetzt ein sechster Kandidat dazukommt, dann schaut die Tabelle so aus:
Es ist also eine 6. Spalte mit 5 Einträgen dazugekommen.
Wenn man weiß, dass es bei 5 Teilnehmern 10 Diskussionen gibt, dann kommen für den 6. Teilnehmer 5 Diskussionen dazu und es gibt daher bei 6 Teilnehmern 15 Diskussionen.
Wir können diese Rechnung auch so aufschreiben.
$$1+2+3+4+5=(1+2+3+4)+5=10+5=15$$
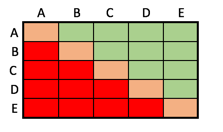
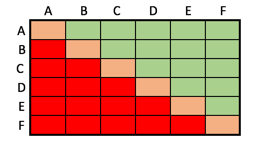
Wir können in den beiden Tabellen auch eine Struktur der (grün markierten) besetzten Zellen erkennen:
Wenn wir die Anzahl der Zeilen und Spalten der beiden Tabellen jeweils mit $n$ bezeichnen, dann hat $n$ bei der kleineren Tabelle den Wert 5 und bei der größeren den Wert 6.
Jede der beiden Tabellen hat dann $n\cdot n=n^2$ Zellen, also $5\cdot 5=25$ bei der kleineren und $6\cdot 6=36$ bei der größeren Tabelle.
Wir müssen die grünen Zellen zählen. Wir nehmen also zuerst die orangen Zellen weg, davon gibts $n$, also 5 oder 6 und es bleiben $n^2-n=n\cdot (n-1)$, also 20 oder 30 Zellen übrig.
Das sind die roten und die grünen Zellen zusammen gezählt.
Wir sehen sofort, dass es in beiden Tabellen genau gleich viele rote und grüne Zellen gibt.
Daher müssen wir nur die Zahl der roten + grünen Zellen halbieren und erhalten dann die Zahl der grünen Zellen. Wir berechnen also $\frac{n\cdot (n-1)}{2}$ für $n=5$ und $n=6$ aus und erhalten $\frac{5\cdot 4}{2}=10$ beziehungsweise $\frac{6\cdot 5}{2}=15$.
Dieses Rezept funktioniert natürlich nicht nur für $n=5$ und $n=6$ sondern für jede beliebige Anzahl $n$.
Wir haben übrigens so ganz nebenbei eine mathematische Formel bewiesen, nämlich
$$1+2+\ldots+(n-1)+n=\frac{n\cdot (n+1)}{2}$$
Wenn man die ganz abstrakte Schreibweise für Summen verwenden will, dann schreibt man
$$\sum_{i=1}^{n}{i}=\frac{n\cdot (n+1)}{2}$$
Davon sollte man sich aber nicht abschrecken lassen, es bedeutet genau dasselbe wie die Formel davor.
(Wenn $n$ die Zahl der Kandidaten ist, dann haben wir eigentlich die Formel $1+2+\ldots+(n-1)=\frac{n\cdot (n-1)}{2}$ bewiesen.)
Wir haben das bewiesen, weil wir die Zahl der grünen Zellen auf zwei verschiedene Arten abgezählt haben und die errechneten Werte daher gleich sein müssen.
Es gibt einen wichtigen Zweig der Mathematik, der sehr oft mit solchen „Abzähltricks“ arbeitet, nämlich die Kombinatorik.
Diese Formel läßt sich auch noch auf eine andere Art beweisen.
Wir schreiben die Zahlen von 1 bis 4 nebeineinder und direkt darunter die Zahlen von 1 bis 4 in umgekehrter Reihenfolge.
Dann ergibt die Summe zweier übereinander stehender Zahlen immer 5 und die gesamte Summe der oberen beiden Reihen der Tabelle ist $5\cdot 4=20$. Die Summer der zweiten Reihe und der ersten Reihe ist aber gleich und daher ist die Summe der ersten Reihe $\frac{20}{2}=10$.
Ebenso ist die Summe der beiden oberen Reihen in dieser Tabelle $6\cdot 5=30$ und daher die Summe der ersten Reihe die Hälfte davon, also $\frac{6\cdot 5}{2}=15$.
Wenn wir die Zahlen von 1 bis 100 addieren wollen, dann geht das natürlich auch nach diesem Rezept und ergibt $\frac{101\cdot 100}{2}=5050$.
Das hat vor ungefähr 230 Jahren schon ein kleiner Volksschüler herausgefunden.
Sein Name war Carl Friedrich Gauss und er wurde später dann einer der berühmtesten und wichtigsten Mathematiker.
Warnung: Diese Erklärungen sind noch nicht zu Ende. Rechnen sie mit einem weiteren Blogeintrag, in dem ich erklären werde, wie man ausrechnet, wieviele Diskussionen es gibt, wenn jede Diskussion 3 oder mehr Teilnehmer haben kann.
Was können Meinungsforscher wissen und was nicht
Gestern ist im ORF und auf Twitter etwas passiert, was es so vorher noch nie gegeben hat.
Frau Dr.$^\textsf{in}$ Eva Zeglovits hat folgendes geschrieben
ich hab soviele unentschlossene in den Daten, dass ich mich gar nix sagen trau
Im ORF (ZiB2 13.4.2016) konnte man folgendes sehen
und hören
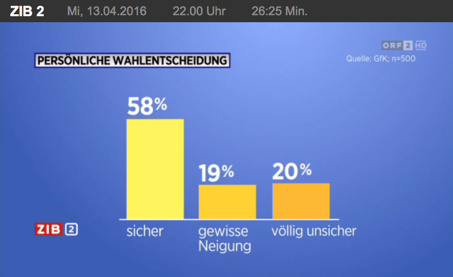
Und wie weit sind die persönlichen Wahlentscheidungen der Österreicherinnen und Österreicher bereits gefallen? 58 Prozent sind sich laut GM Austria-Umfrage schon sicher, wen sie wählen werden, 19 Prozent haben eine „gewisse Neigung“ und 20 Prozent sind noch völlig unsicher.
Diese Aussage beruht auf einer Umfrage von GfK Austria mit 500 Befragten.
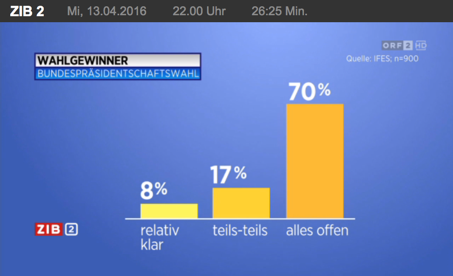
In einer anderen Umfrage (durchgeführt von IFES, 900 Befragte) wurde auch erhoben, ob die Wähler glauben, dass das Wahlergebnis jetzt schon feststünde:
Bei diesen beiden Umfragen ist die Summe der ausgewiesenen Prozentsätze weniger als 100%, es ist also erkennbar, dass nicht alle Befragten eine auswertbare Antwort gegeben haben.
Einen völlig anderen Umgang mit Umfragedaten findet man in einer Tageszeitung:
Diese Umfrage beruht auf eine Stichprobe von 400 Befragten. Selbst wenn das eine saubere Zufallsstichprobe wäre und alle Befragten eine Wahlentscheidung angegeben hätten, betrüge die Schwankungsbreite für die (in der Umfrage vorne liegenden Kandidaten) etwa 4,5%.
Bei der Unsicherheit, die die Umfragen von IFES und GfK Austria zeigen, Umfragedaten ohne den geringsten Hinweis auf statistische Unschärfen und Schwankungsbreiten darzustellen zeigt von einem sehr grundlegenden Missverständnis davon, was statistische Methoden und insbesondere Umfragen, die auf Stichproben beruhen, leisten können.
Es ist ungemein erfreulich, dass der ORF bei dieser Wahl so klar berichtet, dass man aus den Umfragen kaum Prognosen für den Wahlausgang ableiten kann.
Und es ist ebenfalls ungemein erfreulich, dass eine ausgebildete Statistikerin (Frau Dr.$^\textsf{in}$ Eva Zeglovits) die Grenzen der statistischen Methodik dermaßen offen und klar thematisiert.
Sie liefert damit eine wunderbare Illustration der Aussage des bedeutenden Statistikers William Kruskal
Statistics is the art of stating in very precise terms what one does not know
Ziffernnnoten in der Volksschule – ab wann?
Es gibt eine vom Bildungsministerium angestoßene Diskussion darüber, ob man die Ziffernnoten in den ersten drei Volksschulklassen abschaffen soll. Es gibt noch keinen Entwurf für einen entsprechenden Gesetzestext. Der Vorschlag ist also noch nicht bis ins Detail durchdacht.
Zu bedenken – finde ich – ist da Folgendes:
Laut diesem Vorschlag gibts dann in der vierten Volksschulklasse Ziffernnnoten. Die Ziffernnoten dieser Klasse führen zu ganz wichtigen Entscheidungen für das weitere Leben der betroffenen Kinder: von diesen Noten hängt ab, ob die Kinder die Unterstufe einer AHS besuchen dürfen oder nicht.
Grundlage dieser Entscheidung ist das Halbjahreszeugnis. Das ist aus rechtlicher Sicht gar kein Zeugnis (es gibt kein Rechtsmittel dagegen), und es ist die erste zumindest halboffizielle Ziffernbenotung für alle Kinder.
Die Kinder werden also zur Halbzeit der vierten Klasse erstmals mit Ziffernnnoten beurteilt, und davon hängt ihre weiter Bildungskarriere ab.
Sie wurden vorher niemals verpflichtend mit Ziffernnoten beurteilt. Sollte man da nicht vorher zumindest einmal schon mit Ziffernnoten beurteilt haben, damit Kinder und Eltern sich darauf einstellen können, was da auf sie zukommt, wenn es dann um eine Weichenstellung für das weitere Leben geht?
Wäre es also nicht besser, Ziffernnoten „zum Drangewöhnen“ auch schon in der dritten Klasse zu vergeben?
Natürlich ist auch eine Schule ohne Ziffernnoten denkbar. Aber solange die Entscheidung über die AHS-Reife von Ziffernnoten abhängt scheint es mir schon ziemlich hart, diese Form der Beurteilung das erste Mal genau bei dieser extrem wichtigen Bildungsentscheidung einzusetzen, und noch dazu in einer Form, die den rechtlichen Spielraum der Eltern sehr eng hält.
Anscheinend hat dieser Vorschlag noch Verbesserungspotential!