Warum Statistiker nach Wahlen leiden müssen

Nach jeder Wahl wird analysiert, welche Wählergruppe sich wie auf die Parteien verteilt hat. Auch nach der Landtagswahl 2013 in Tirol ist das so.

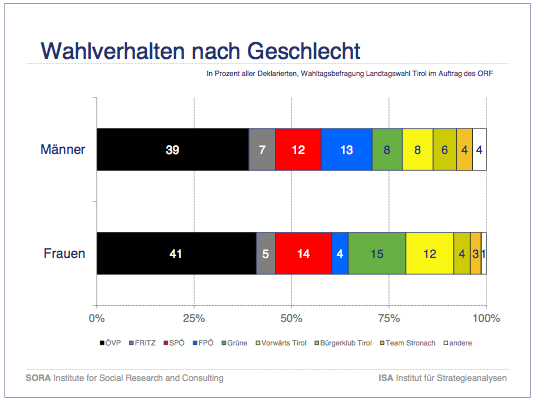
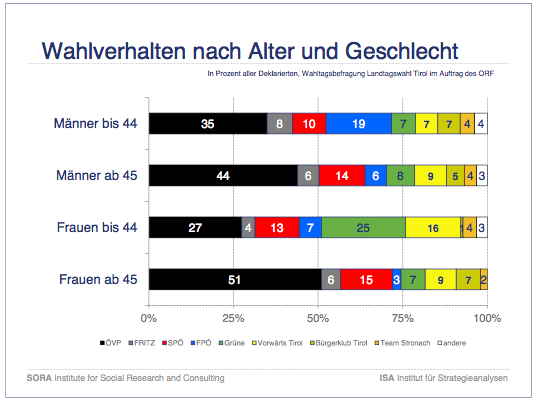
Hier 2 Beispiele solcher Analysen:

Diese Grafiken finden sich in der Wahlanalyse von ISA und SORA

Die zweite Analyse wird auf der Facebook-Seite von Christoph Chorherr heftig diskutiert.

Einem Statistiker fällt auf, daß bei keiner der beiden Grafiken die statistische Schwankungsbreite der Parteienanteile angegeben wird. In der ISA-SORA-Analyse findet man einige Zahlen zu dieser Fragestellung; allerdings findet man leider nicht alle Zahlen, die man braucht, um die Schwankungsbreite der Anteile in den obigen beiden Grafiken ausrechnen zu können.

Mit etwas Detektivarbeit kann man allerdings die Schwankungsbreiten doch annähernd berechnen.
Die Anzahl der Befragten ist n=1227. Laut Angaben wurden die Daten nach Geschlecht, Alter, Bildung und Erwerb gewichtet, die zu einer Überprüfung notwendigen Zahlen stehen aber nicht öffentlich zur Verfügung. Zur Abschätzung der Schwankungsbreiten kann man aber zunächst einmal auch diese Schwankungsbreiten für ungewichtete Schätzwerte berechnen.

n=1227 ergibt eine Schwankungsbreite von maximal 2,8% für geschätzte Anteile an der Grundgesamtheit aller Wahlberechtigten, und diese Zahl findet man auch in der zitierten Quelle. In den Analysen unserer Grafiken geht es aber um Anteile an Männern, Frauen, und auch noch nach Altersgruppen unterteilten Gruppen von Männern und Frauen. In diesen Grafiken werden außerdem nur Anteile an deklarierten Wähler ausgewiesen, also ist die Grundgesamtheit in diesem Fall die Grupper der deklarierten Wähler. Bei eine Wahlbeteiligung von weniger als 60 Prozent ist also für diese Untersuchungen die Stichprobengröße etwa 700. Sollte es außer den Nichtwählern auch Befragte gegeben haben, die zwar gewählt, sich bei der Umfrage aber nicht deklariert haben, dann kann die relevante Stichprobengröße auch nur 550 betragen. Dabei nehmen wir eine Nichtdeklarationsquote von 20% der Wähler an, was laut Auskunft von Meinungsforschern durchaus immer wieder vorkommt.

Gehen wir nun bei unseren weiteren Rechnungen von einer Stichprobengröße 600 für die deklarierten Wähler aus.

Etwa die Hälfte der Wähler sind jeweils Männer und Frauen (das stimmt zwar nicht genau, ist aber genau genug für die Berechnungen der Schwankungsbreiten).
Wenn wir also die Schwankungsbreiten der Parteienanteile bei Männern und Frauen berechnen, dann ergibt sich 5,8%. Damit man davon reden könne, dass der Anteil der ÖVP bei den Männern signifikant verschieden vom Anteil bei den Frauen ist müsste die Differenz in der Stichprobe sogar 8,2% betragen. Nach solchen Berechnungen stellen sich die Geschlechterdifferenzen nur bei den Grünen und bei der FPÖ als signifikant heraus.

Noch größer sind die statistischen Schwankungsbreiten bei der Einteilung nach Geschlecht und Alter. Die 4 untersuchten Gruppen sind annähernd gleich groß. Genau genommen ist die Gruppe der Frauen über 44 etwas größer als die 3 anderen Gruppen, aber der Unterschied ist so klein, dass wir ihn für unsere Berechnungen außer acht lassen können.

Bei 600 deklarierten Wählern ist also jede der 4 Teilgruppen etwa 150 Wähler groß.
Die statistische Schwankungsbreite ist dann maximal 8,1%. Die maximale Schwankungsbreite für einen Anteilsunterschied in 2 Gruppen ist dann 11,5%. Der Unterschied der ÖVP-Anteile zwischen älteren und jüngeren Männern beträgt 9%, ist also statistisch nicht signifikant und sollte daher nicht als politisch relevant interpretiert werden. Der entsprechende Unterschied zwischen den älteren und den jüngeren Frauen ist größer 11,5%, er ist also statistisch signifikant und politisch relevant.
Etwas vergröbernd kann man sagen, dass ganz generell die Unterschiede zwischen älteren und jüngeren Frauen statistisch signifikant sind, entsprechendes für die Männer aber nicht gilt.

Ganz wichtig ist folgendes:
In den untersuchten (und vielen ähnlichen) Grafiken steckt hinter jedem der aufgeteilten Balken eine andere Stichprobe mit jeweils anderer Anzahl von Befragten. Die Schwankungsbreite der geschätzten Anteile kann man nur berechnen, wenn man die Stichprobengröße kennt. Daher wäre es ein Gebot der Sauberkeit, diese Zahl auch bei jedem „Aufteilungsbalken“ anzugeben.

Wenn diese Zahlen aber fehlen, dann kann bei statistisch nicht ganz fachkundigen Lesern der Eindruck entstehen, dass die Größe der gesamten Stichprobe (n=1227) auch die Schwankungsbreite der Parteienanteile in Untergruppen bestimmt. Das ist aber, wie wir gesehen haben, definitiv nicht der Fall.

Lange Zeit wurden bei Meinungsumfragen nicht einmal die Gesamtstichprobengrößen ausgewiesen. Wir Statistiker haben uns das immer gewünscht. Dieser Wunsch wird uns in letzter Zeit auch schon erfüllt.

Jetzt erweitern wir die Wunschliste: Wenn es um Parteienanteile in Untergruppen der Wahlberechtigen geht (z.B. Altersgruppen), dann wüssten wir auch gerne die Stichprobengrößen für diese Untergruppen.
Erst so können politisch interessierte Leser die Zuverlässigkeit von Aussagen über Untergruppen halbwegs abschätzen.

Und noch einen inhaltlichen Wunsch habe ich. Die Nichtwähler waren bei dieser Wahl schon die größte Wählergruppe. Eine Aufgliederung des Nichtwähleranteils nach Alter und Geschlecht wäre meiner Meinung nach eine der interessantesten Analyse nach dieser Wahl. Leider ist die bei den Analysen von ISA-SORA nicht dabei.

Schlagwörter: Statistik, Wahlen

Was kann man aus Meinungsumfragen erschließen und was nicht?

Im Jahr 2013 kommen einige Wahlen und Volksbefragungen auf uns zu. Im Jänner die Volksbefragung zur Wehrpflicht, spätestens im Oktober die Nationalratswahl, und vorher schon Landtagswahlen in Kärnten, Niederösterreich und Tirol. In Deutschland gibt’s Landtagswahlen in Niedersachsen, Bayern und Hessen und im September die Bundestagswahl. Daher liest und hört man immer wieder die Ergebnisse und […]

Schlagwörter: Statistik, Wahlen